Finding Tension in a Rod Attached to Sliding Blocks

[Inaki kemasda]

Homework Statement

A thin rod AB of weight W is attached to two blocks A and B that slide freely in the railways represented. The blocks are linked by a string inextensible and without weight passing through a pulley C.
Express the tension in the string in function of W and the angle θ that forms the bar and the horizontal.

Homework Equations

sum of the moments respect to C:
W*cos(theta)*L/2+Fx*sin(theta)*L+Wa*cos(theta)*L-Fy*cos(theta)*L=0
where L is the length of the rod and F the reaction of the rod.
sum of forces in horizontal and vertical:
Fx=T
Fy=Wa+W
is this correct?

The Attempt at a Solution

The solution from the professor is T=W/(2*(1-tan(theta)) and the one i find is: T=W/(2*tan(theta)) similar, but not the same. Help please! thank you so much.

 

[collinsmark]

Hello Inaki kemasda,

Welcome to Physics Forums!

sum of the moments respect to C:
W*cos(theta)*L/2+Fx*sin(theta)*L+Wa*cos(theta)*L-Fy*cos(theta)*L=0
where L is the length of the rod and F the reaction of the rod.

Forgive me for not following your equation on that. Part of the reason I might be having trouble following your logic is that when I solved the problem, I found it unnecessary to take the moment around point C.

As a matter of fact, I didn't take the moments of anything. I did the problem simply by summing the x-component of all the forces involved, summing the y-components of all the forces involved, and then combining equations.

I concede though, I took a shortcut regarding the rod's weight, and how that relates to the vertical force. To find mathematically, you could take the moment of the rod around point B.

Consider the rod's weight. Part of the rod's weight will be held up by the tension of the string at point A. But the other part of the rod's weight is held up by the normal force on point B (the track itself). But the force at point B, that's holding up a fraction of the rod's weight, doesn't affect the tension in the string. It's an external force that isn't part of this problem. On the other hand, the string's tension at point A holds up the rest of the rod's weight.

You can use one of two methods to calculate this part of the tension at point A that is associated with with rod's weight. (1) You could use common sense. (2) you could take the moment around point B, which gives you the same result in the end.

sum of forces in horizontal and vertical:
Fx=T

That much is correct, yes!

Fy=Wa+W

What's Wa? I think we're supposed to assume that the blocks are massless. The only thing that has any mass or weight in this problem is the rod, which has a weight of W.

But you forgot to express the tension of the string at point A. The tension plays a part too!

Also, the entire weight of the rod W is not held at point A. Only a fraction of its weight is held up by point A. The other part of the weight is held up by point B. So concerning the weight of the rod in isolation, how much is supported at point A and how much at point B?

The Attempt at a Solution

The solution from the professor is T=W/(2*(1-tan(theta)) and the one i find is: T=W/(2*tan(theta)) similar, but not the same. Help please! thank you so much.

I ended up with the same answer that your professor gave.

[Edit: corrected a typo above. Accidentally typed "C" when I meant "A."]

 

[Inaki kemasda]

Thank you collinsmark! I'm very grateful for your welcome.
I think i understand now.
sum forces in x: Fx=T
sum forces in y: Fy+T=W/2
because we can assume that the weight is distributed half and half between A and B, right? and then, for finish we need only realize that: tan(theta)=Fy/Fx
Then we get to: T=W/(2*(1+tan(theta)))
i found that the original solution proposed by the professor: T=W/(2*(1-tan(theta))) must be wrong because in theta=45 degrees there's a nonsense singularity. also, if we plot both solutions, we see that only the first has physical sense.
it's this right?
Thank you so much for your time and energy collinsmark :)
yours truly, iñaki

 

[collinsmark]

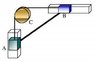
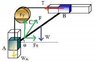
Keep your directions consistent. For the horizontal components, let's define the positive x-axis (right) as the positive direction, and the positive y-axis (up) as the positive direction for the vertical direction.

sum forces in x: Fx=T

Yes, this is correct because there is a positive reaction force (due to the rod), F_x, directed toward the right.

The tension force T is directed toward the left (making it negative).

Since nothing is moving (the system is in static equilibrium), the forces must sum to zero. So we have,

F_x - T = 0.​

sum forces in y: Fy+T=W/2

I think something went wrong with your directions here. In truth it depends on how you define F, so it might still be valid, but you must be consistent.

If we define F_y as a positive value (which is quite reasonable, since we defined F_x as a positive value above), this force is pushing in the down direction. The weight is also pushing in the down direction. The tension is up. So that gives us,

T - F_y - W/2 = 0.​

because we can assume that the weight is distributed half and half between A and B, right?

Yes, I'm pretty sure that we are supposed to assume that the rod's center of mass is at the rod's center. Taking a moment around some point (point B would be a good choice, but you could choose some other point if you wish) shows that the vertical force due to the rod's weight at point A is W/2.

and then, for finish we need only realize that: tan(theta)=Fy/Fx
Then we get to: T=W/(2*(1+tan(theta)))
i found that the original solution proposed by the professor: T=W/(2*(1-tan(theta))) must be wrong because in theta=45 degrees there's a nonsense singularity. also, if we plot both solutions, we see that only the first has physical sense.
it's this right?

You might want to re-do that. Again, the answer I got was the same as your professor's answer,

T = W/(2(1 - tanθ))​

Regarding the singularity at 45^o:

This actually makes sense to me at the present. If θ is ever greater than 45^o, the tension required in the string becomes negative. In other words, if it remains operating as a "string" operates (where you can pull on it, but not push), what happens is that it will not keep the upper block B from moving to the left. What would happen, is that the string simply ceases to being taught (becomes slack), and slides off the pulley C, and the block B slides right above pulley C where it eventually comes to rest (leaving the string completely loose and just hanging somewhere without any tension).

For the case where θ is less than zero, but approaching 45^o, it is approaching an angle where it has infinite leverage. Beyond that point, the string becomes slack as discussed above. Before that point (where θ is less than 45^o) its leverage increases up to infinity as θ approaches 45^o. That explains the singularity in the equation at θ = 45^o.

Further advice:

Go back up to the force equations described above, and note that
F_x = Fcosθ
F_y = Fsinθ

 

[Inaki kemasda]

oook! i got it! many thanks my friend :)