Nat1234123
- 6
- 0
- Homework Statement
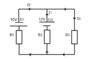
- Which current ratings do I1, I2 and I3 have if the resistances hold R1 = 0.1 ohm, R2 = 0.02 Ohm and R3 = 0.2 Ohm?
- Relevant Equations
- U = IR
1/R = 1/R_1 + 1/R_2 + ....
I1 = I2 + I3
In my attempt, I tried
1) I1 = I2 + I3
Then set up these two equations based on Kirchhoff's second rule:
2) U1 = R1 (I2) + R3 (I3) and
3) U1 + U2 = R1 (I1) + R2 (I3).
From what we have
10 = 0.1* I_2 + 0.2 * I_3
22 = 0.1* I_2 + 0.02*I_3
I_3 = 50 - 0.5 I_2
That means
I_2 = 233.3 A
I_3 = -66.7A
I1 = 166.6A
My answer is completely off.
1) I1 = I2 + I3
Then set up these two equations based on Kirchhoff's second rule:
2) U1 = R1 (I2) + R3 (I3) and
3) U1 + U2 = R1 (I1) + R2 (I3).
From what we have
10 = 0.1* I_2 + 0.2 * I_3
22 = 0.1* I_2 + 0.02*I_3
I_3 = 50 - 0.5 I_2
That means
I_2 = 233.3 A
I_3 = -66.7A
I1 = 166.6A
My answer is completely off.