Endevor
- 3
- 0
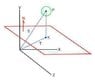
Ok, I've been stewing on this problem for a couple weeks now, and it's primarily due to my lack of practice with vectors, but I'm learning how to work with 3D computer graphics and trying to determine when an object hits a plane. Given the normal of the plane N=[nx,ny,nz] and the point at the center of my sphere, P=(px,py,pz), how do I find the distance from the Point at the center of the sphere to the plane?
From what I understand, there's some way to do it using the origin 'O' to find the point K along a vector T. We also know a vector S from O to point P. Where I'm stuck right now is finding K. If I can find Rp, then I can use T+Vector(Goal)=S.
I may be going about this a completely wrong way, in which case, ignore my short thoughts and use what I wrote above. I just need some help on how to approach this.
From what I understand, there's some way to do it using the origin 'O' to find the point K along a vector T. We also know a vector S from O to point P. Where I'm stuck right now is finding K. If I can find Rp, then I can use T+Vector(Goal)=S.
I may be going about this a completely wrong way, in which case, ignore my short thoughts and use what I wrote above. I just need some help on how to approach this.