- #1
nhartung
- 56
- 0
I'm reviewing for my physics final and going over all of my old exams. I'm trying to figure out how to do this question that I got wrong.
Six charges that are equal in magnitude, 0.48µC are arranged in a hexagon where each charge is r = 1.4 m from the center. Two of the charges are positive, and four charges are negative.
(i) What is the electric field at the origin?
(ii) What is the electric potential at the origin?
E = kq/r2
V(Electric Potential) = kq/r
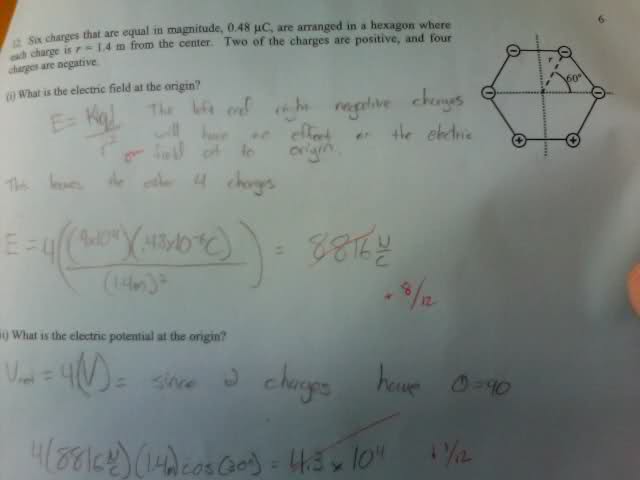
In (i) I'm not sure what I'm going wrong, although the answer does seem pretty huge but I'm doing it just like the examples in the book.
In (ii) I'm pretty sure I forgot the equation on the exam which should be V = kq/r.
Again, if I do this I get a large answer 4(9.0x10^9)(.48µC)/1.4m = 12,342.
Homework Statement
Six charges that are equal in magnitude, 0.48µC are arranged in a hexagon where each charge is r = 1.4 m from the center. Two of the charges are positive, and four charges are negative.
(i) What is the electric field at the origin?
(ii) What is the electric potential at the origin?
Homework Equations
E = kq/r2
V(Electric Potential) = kq/r
The Attempt at a Solution
In (i) I'm not sure what I'm going wrong, although the answer does seem pretty huge but I'm doing it just like the examples in the book.
In (ii) I'm pretty sure I forgot the equation on the exam which should be V = kq/r.
Again, if I do this I get a large answer 4(9.0x10^9)(.48µC)/1.4m = 12,342.