Finding the electric field of a electric quadrupole

[n387g]

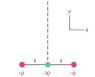
One type of electric quadrupole consists of two dipoles places end to end with their negative charges (say) overlapping; that is, in the center is -2Q flanked (on a line) by a +Q to either side. Determine to electric field, E, at points along the perpendicular bisector and show that E decreases as 1/r⁴. Measure r from the -2Q charge and assume r>>l.


E+=E-=(1/4\pi\epsilon₀)*(Q/(r²+(l²/4)
p=Ql

The Attempt at a Solution

First I broke the electric fields into the x and y axes.
Where, E_x=0
For the E_y, I used the equation E=(1/4\pi\epsilon₀)*(p/r³)
Then, substituted p for (Q*l) and then r³ for r⁴
I assume there must be more to it than that, but I'm at a loss.

 

[cupid.callin]

E+ is not = E-

 

[n387g]

Okay, so you have to add the electric fields at the +Q, -2Q and +Q.
So for +Q, E=k(Ql/(l²+r²)^(1/2)) (cos(theta)r_x+sin(theta)r_y)
And the for -2Q, E=k(2Ql/r²)(sin(theta)r_y)
And for the other +Q, E=k(Ql/(l²+r²)^(1/2)) (-cos(theta)r_x+sin(theta)r_y)
Is this the correct way to do this?

 

[cupid.callin]

+Q, E=k(Ql/(l²+r²)^(1/2)) (cos(theta)r_x+sin(theta)r_y)

Whats that l after Q

 

[n387g]

it's a lowercase L, for length

 

[n387g]

Using the equation where p=Ql

 

[SammyS]

Do you know about Taylor Series ?