slash
- 1
- 0
I have a heavy bag and I was wondering if I could find out how much force is applied when I kick it. Here's a picture describing of the problem:
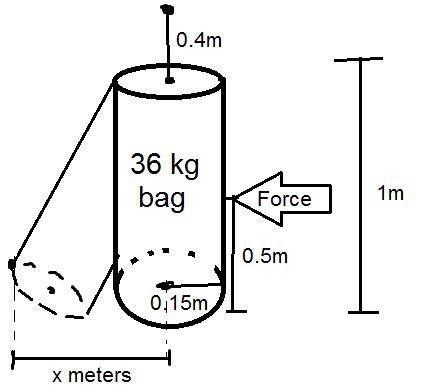
If some amount of force is applied that causes the bag to move x meters (first swing) in the direction of the force, how much was applied? The bag is cylindrical, with a radius of 0.15m and a height of 1m. It has a mass of 36 kg and is hanging 0.4m away from a point by chain.
I don't think the speed/acceleration of the bag is necessary because requiring either of those things suggest that there's more than one value for force that would cause the bag to move a certain amount. Wouldn't the bag just move farther and farther as more force was applied?
Something that I think is important that I currently do not know is how elastic (is that what it's called?) the surface of the bag is (that is, how much the bag "caves in" on itself when hit), so just assume something reasonable.
Thanks! If there's any information you need about the situation then ask and I'll supply everything I can.
If some amount of force is applied that causes the bag to move x meters (first swing) in the direction of the force, how much was applied? The bag is cylindrical, with a radius of 0.15m and a height of 1m. It has a mass of 36 kg and is hanging 0.4m away from a point by chain.
I don't think the speed/acceleration of the bag is necessary because requiring either of those things suggest that there's more than one value for force that would cause the bag to move a certain amount. Wouldn't the bag just move farther and farther as more force was applied?
Something that I think is important that I currently do not know is how elastic (is that what it's called?) the surface of the bag is (that is, how much the bag "caves in" on itself when hit), so just assume something reasonable.
Thanks! If there's any information you need about the situation then ask and I'll supply everything I can.