Finding the intersect of two functions

[stevemilw]

I have the following equation which describes a water jets trajectory.

Vx=Cos(50) * 6.5m/s
Vy=Sin(50) * 6.5m/s

x=Vx*t
y=Vy*t-0.5*g*t^2

where t=time

Now, this plots a curve very well starting from zero.

I want a line, starting from 0 also, that intersects the curve.
Now, I have used the equation y=tan(35)*x where x is the distance across the bottom of the graph (x axis) on the adjacent part in the trig.

So, to find the intersect, i need to get the curve equation in terms of x and y instead of y and t, so i have re-arranged; t=x/Vx and subbed into give;

y=Vy*(x/Vx)-0.5*9.81*(x/Vx)^2

If I equal them to one another; tan(50) *x = Vy*(x/Vx)-0.5*9.81*(x/Vx)^2
and re-arrange for x, i get;

(tan(35)*Vx^2)/(-0.5*g)) - ((-Vx*Vy/(0.5*g)) = x = 0

Now, there is an intersect at 0, but not the one i want.

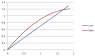
Attached is a graph of both the line and curve, with 50 degrees angle on the jet, and 35 degrees on the line.

Please help, I've been stuck on this alllll day, and a lot of yesterday too!

 

[HallsofIvy]

That's a quadratic equation. It has two solution of which x= 0 is one. What is the other?

 

[stevemilw]

Its not a quadratic equation because it can't be put into the form of ax^2+bx+c=0 since we have an x on both b and c, so what i have is ax^2+bx+cx=0.

 

[HallsofIvy]

Which is equal to ax^2+ (b+ c)x= 0, a quadratic equation. As I said, x= 0 is one solution, what is the other.

 

[stevemilw]

Okay, so where we have a =(0.5*9.81)/(Vx^2) = 0.2929
b =Vy/Vx = 1.19175
c=TAN(35) in degrees

Plugging it all in and checking with calculator and excel, i get x=-0.7119 and x=-3.3568

Neither of which are the intersection.
Also, it is not referring to t or time, because the time range is only from 0-0.5

 

[stevemilw]

In the previous comment, i assumed ax^2+bx+cx=0 since that's the form of my equation.
If i calculate, by transforming my equation to ax^2+bx+c=0 by adding both a and b together (because they both have one x) and making it b, and then making c = 0, i get x=0 (promising) but then x=-6.459 which is incorrect.
Driving me insane. I hate not being able to solve a problem.
I will ask my tutor, but she's not in till next week. If anyone has any ideas then please comment.

 

[Ray Vickson]

In the previous comment, i assumed ax^2+bx+cx=0 since that's the form of my equation.
If i calculate, by transforming my equation to ax^2+bx+c=0 by adding both a and b together (because they both have one x) and making it b, and then making c = 0, i get x=0 (promising) but then x=-6.459 which is incorrect.
Driving me insane. I hate not being able to solve a problem.
I will ask my tutor, but she's not in till next week. If anyone has any ideas then please comment.

Check the sign of 'a'.

 

[stevemilw]

Check the sign of 'a'.

Thanks, i tried subtracting c from b and i got the correct answer! It wasn't the sign of a, i had just simply got the signs wrong, but you pushed me in the right direction.
Seems very simple now!