Finding the minimum frequency

[Saitama]

Homework Statement

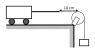
A heavy string is tied at one end to a movable support and to a light thread at the other end as shown in figure. The thread goes over a fixed pulley and supports a weight to produce a tension. The lowest frequency with which the heavy string resonates is 120 Hz. If the movable support is pushed to the right by 10 cm so that the joint is placed on the pulley, what will be the minimum frequency at which the string can resonate?

Homework Equations

The Attempt at a Solution

When the light string is completely hanging down, the minimum frequency of the heavy string can be found by considering the case of a string clamped at both ends and vibrating in the fundamental mode. I am not sure what happens when a part of light string is not hanging. Does the heavier string oscillates with one of its end clamped and the other being free? I don't know how to proceed here.

Any help is appreciated. Thanks!

 

[CWatters]

I am not sure what happens when a part of light string is not hanging. Does the heavier string oscillates with one of its end clamped and the other being free?

Yes.

You get a node at the cart end and an antinode at the end that isn't fixed (eg the light string end).

 

[Saitama]

Yes.

You get a node at the cart end and an antinode at the end that isn't fixed (eg the light string end).

Thanks CWatters!

I did try this before posting the problem here and was not getting the right answer. I then realized that I have read the question incorrectly. I interpreted that the string is pulled up to a length of 10 cm in second case.