subbby
- 22
- 0
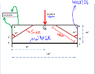
Please find the attached picture. It clearly explains the problem
What is the method to find the size of the knee braced beam member?
Do we have to to draw free body diagram for each point and then find out the force acting on the cross member-then see if that beam's cross section area can withstand the derived force?
Or
is (33069 # /2 )* Cos 45 the force on each cross member beam ?
What is the method to find the size of the knee braced beam member?
Do we have to to draw free body diagram for each point and then find out the force acting on the cross member-then see if that beam's cross section area can withstand the derived force?
Or
is (33069 # /2 )* Cos 45 the force on each cross member beam ?