dGasim
- 16
- 0
Homework Statement
A woman walks due west on the deck of a ship at 3 mi/h. The ship is moving north at a speed of 23 mi/h. Find the speed and direction of the woman relative to the surface of the water. (Round your answers to one decimal place.)
Homework Equations
The Attempt at a Solution
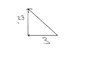
First I drew the picture:
EDIT: Attachment
Then I solved the relative velocity formula:
v_{w/g} = v_{s/g} + v_{w/s} = 23 + 3 = 26mi/h
Which went wrong, so I made another attempt:
\sqrt{23^2 + 3^2} = 23.2
And i don't know how to find the angle. Should I do it like arctan(23/3) ?
Thanks in advance,
Gasim Gasimzada