sony
- 102
- 0
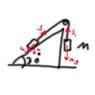
"A brick (M) is connected to another brick on a 30 degree slope. Don't mind the weight of the rope connecting these, and the friction.
The mass of the right brick (M) is 3,5 kg
What is the speed of the brick (M) when it have falled 0,5m?"
I've drawed forces on the illustration.
Here is a picture of what I've done (I wrote it in mathtype, I don't know how to paste it here)
http://home.no.net/erfr1/images/1.gif
I just don't understand how to find the acceleration without knowing both masses.
Thank you for your help!
The mass of the right brick (M) is 3,5 kg
What is the speed of the brick (M) when it have falled 0,5m?"
I've drawed forces on the illustration.
Here is a picture of what I've done (I wrote it in mathtype, I don't know how to paste it here)
http://home.no.net/erfr1/images/1.gif
I just don't understand how to find the acceleration without knowing both masses.
Thank you for your help!
Attachments
Last edited by a moderator: