Finding the Sum of Perpendiculars in a 24-Sided Polygon Inscribed in a Circle

[armolinasf]

Homework Statement

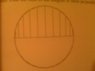
There is a regular 24 sided polygon inscribed in a circle. A diameter is drawn and perpendiculars are dropped from all the vertices on that side of the diameter. Find the sum of the lengths of the perpendiculars.

The Attempt at a Solution

I came across this problem and I have no clue how to approach it. I'm looking for a point in the right direction. Thanks for the help!

 

[tiny-tim]

hi armolinasf!

well, what formula are you starting with?

 

[armolinasf]

No formula was given. It was at the end of a section on trig identities, specifically using them to sum trig series.

 

[ehild]

You have to find the formula. You have studied trigonometry haven't you?

ehild

 

[armolinasf]

My first instinct was to write something like S=r+2(l1+l2+l3+l4+l5), where l is the length of each chord. Should I be looking for a way to express each l in terms of r?

 

[tiny-tim]

hi armolinasf!

yes, and the various angles (nπ/12)

 

[armolinasf]

Yeah i finally realized that the height of each perpendicular is equal to the sine of the angles...So here my sum:

S=r+2r[sin(pi/12)+sin(pi/6)+sin(pi/4)+sin(pi/3)+sin(5pi/12)]

 

[tiny-tim]

hi armolinasf!

(have a pi: π and a sigma: ∑ )

ok, so the answer to my original question …

well, what formula are you starting with?

is r∑_n=1…12 sin(nπ/12) …

now calculate that using either standard https://www.physicsforums.com/library.php?do=view_item&itemid=18"