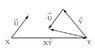
thereddevils said:
the vector is not in the direction of i and j instead its placed at angle, don't we need to resolve first?
Also, if the relative velocity is simply u-v ,then the answer wouldn't be interms of a and b too. Btw the answer given is in terms of u,v,a and b.
Whether a vector is in the direction of
i or
j depends on which directions
i and
j point in. They aren't mentioned in the problem statement, so I guess that's up to you. A convenient choice might be to make
i parallel to the displacement vector from ship X to ship Y. Then
\textbf{i}=\frac{\vec{XY}}{|\vec{XY}|} \enspace\enspace\enspace \textbf{j}=\frac{\textbf{u}-(\textbf{u}\cdot\textbf{i})\textbf{i}}{|\textbf{u}-(\textbf{u}\cdot\textbf{i})\textbf{i}|}
and
\textbf{u}=|\textbf{u}| \, \cos(a) \, \textbf{i}+|\textbf{u}|\,\sin(a) \,\textbf{j}
\textbf{v}=-|\textbf{v}| \, \cos(b) \, \textbf{i}+|\textbf{v}|\,\sin(b) \,\textbf{j}
Then you could define a relative velocity
r, with respect to ship X, as
\textbf{r}=\textbf{v}-\textbf{u}=-(|\textbf{v}|\cos(b) + |\textbf{u}| \cos(a) ) \textbf{i}+(|\textbf{v}|\sin(b)-|\textbf{u}|\sin(a)) \,\textbf{j}
and, having defined basis vectors
i and
j, you can get the tangent of the angle you're after using just the dot product and the definition of the tangent of an angle as its sine divided by its cosine.