Finding the transfer function (H(jw)) of a sinusoidal-input circuit

[college321]

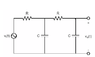
1. Find the transfer function of the following circuit. The circuit has been included as an attachment. I have tried using node voltage, which leads me to this equation:
(V1 - Vi)/R + V1/C + (V1-Vo)/(R+C) = 0

*V1 is the voltage of the essential node on the top center of the circuit.

I thought this would work but I am having trouble finding a way to get the Vo/Vi ratio. I know the C values need to be converted into the S-domain, but that isn't what I'm confused about. Any suggestions?

 

[gneill]

You would have to solve your equation for the node voltage V1, then treat the final RC combination as a voltage divider to find Vo in terms of Vi.

Alternatively, treat Vo as another node and write two equations. Solve for Vo.

 

[college321]

Ok, so I'm trying the idea of treating Vo as another node, but how exactly would that work?

Would the new equation be this:

(Vo-V1)/R + Vo/C = 0 ?

This is the only way I could think of making an equation using this method, but I'm 99.9% sure that's wrong. Could you help me out?

 

[gneill]

That looks fine. You'll have to re-write the last term in your first equation, too, in order to take into account this new node.

The idea is that you will have two equations in two unknowns, V1 and Vo. Solve for Vo.

 

[college321]

Ooooohhhhh, I didn't know I would need to adjust the first equation. Now it makes sense. Thank you!

 

[rude man]

Ok, so I'm trying the idea of treating Vo as another node, but how exactly would that work?

Would the new equation be this:

(Vo-V1)/R + Vo/C = 0 ?

This is the only way I could think of making an equation using this method, but I'm 99.9% sure that's wrong. Could you help me out?

That doesn't look "fine" to me. The dimensions of each term in your equation must be the same ...

 

[gneill]

That doesn't look "fine" to me. The dimensions of each term in your equation must be the same ...

The OP stated in the first post of the thread that he was letting the component names stand in for their impedances, that they would be converted to s-domain values anon.

 

[rude man]

The OP stated in the first post of the thread that he was letting the component names stand in for their impedances, that they would be converted to s-domain values anon.

Not what he said. He said "C values". That sounds like Farads to me. And even if he meant impedances it would be a wrong equation, since capacitive impedance is 1/wC by definition unless the s transformation is included.

We're dealing with students & I think they should be encouraged to write sensible equations.

 

[gneill]

Not what he said. He said "C values". That sounds like Farads to me. And even if he meant impedances it would be a wrong equation, since capacitive impedance is 1/wC by definition unless the s transformation is included.

We're dealing with students & I think they should be encouraged to write sensible equations.

While I agree that beginning students should be encouraged to follow the standard forms in all their glory, I noted what the OP implied by his shorthand and went with it; I didn't take him literally when he said 'C values', meaning only the capacitances, I took it to mean the reactive components in general; it sure looked like he knew the difference between component values and their impedance when he talked about their s-domain values. It's equivalent to writing ZC and ZL for the component impedances and replacing them by 1/(jωC) and jωL later on.

The actual impedances of the components can be substituted after the simultaneous equations are solved, and the expression cleaned up then. Yes, using L and C to represent the impedances is notationally "impure", but it's not a hanging offense as long as it's not submitted for marking in that form

 

[rude man]

While I agree that beginning students should be encouraged to follow the standard forms in all their glory, I noted what the OP implied by his shorthand and went with it; I didn't take him literally when he said 'C values', meaning only the capacitances, I took it to mean the reactive components in general; it sure looked like he knew the difference between component values and their impedance when he talked about their s-domain values. It's equivalent to writing ZC and ZL for the component impedances and replacing them by 1/(jωC) and jωL later on.

The actual impedances of the components can be substituted after the simultaneous equations are solved, and the expression cleaned up then. Yes, using L and C to represent the impedances is notationally "impure", but it's not a hanging offense as long as it's not submitted for marking in that form

Let us agree to disagree.