Finding the Unknown Angle in Equilibrium for Symmetrical Bars Under Load

In summary, the problem involves finding the angle u of two symmetrical bars in equilibrium under a load, with a spring at the midpoint and a block on a sloped ground. Using the equations of equilibrium and a free body diagram of the block, the unknowns Ax, Ay, u, and N were determined, leading to a quadratic equation for tan(u). The closest reasonable value obtained was approximately 56.1 degrees, but this value did not work when applied to the problem. The question of whether the 45 degree angle is relative to the other bar or the vertical was clarified, with the conclusion that it is relative to the horizontal.
  • #1
Karstedt
4
0

Homework Statement



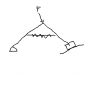
Trying to find angle u of bars (symmetrical) with ground at equilibrium under load.
Two bars, negligible weight of length .4m
Spring at midpoint k = 3kN/m, unstretched when bars at 45 deg
F = 150N, 5 deg
W of block 10kg
Slope of ground under block 5 deg
coef friction = .2

Homework Equations



Fx = 0 = Ax + 150sin5 - Nsin5 - .2Ncos5
Fy = 0 = Ay - 150cos5 + Ncos5 - .2Nsin5
Ma = 0 = 150cos5*.4cosu + 150sin5*.4sinu - Ncos5*.8cosu + .2Nsin5*.8cosu

The Attempt at a Solution



4 unknowns, Ax, Ay, u, N... this course doesn't include indeterminate structures so I tried anyway. Since I could not get an answer via the standard eq equations I tried to eliminate a variable first in the whole structure then by doing a FBD of the block. I got N in terms of u but it still doesn't work anything out. It's incredibly messy using the block FBD and I re-did it several times because I kept finding errors but I eventually got to a quadratic of tan(u) that spit out ~56.1 deg. which is the closest thing to a reasonable value I've gotten, but that value doesn't seem to work when I run with it. I tried to find a trig identity that would simplify things, but can not work anything out.
 

Attachments

  • machine.png
    machine.png
    1.3 KB · Views: 423
Physics news on Phys.org
  • #2
That 45°, is it relative to the other bar or relative to the vertical?
 
  • #3
It's relative to the horizontal actually... but at 45 that's the same as vertical. The angles of both bars relative to the horizontal ground.
 

FAQ: Finding the Unknown Angle in Equilibrium for Symmetrical Bars Under Load

What is an unknown angle in equilibrium?

An unknown angle in equilibrium refers to an angle in a system that is in balance or at rest, but the specific value of the angle is not known.

Why is it important to know the unknown angle in equilibrium?

Knowing the unknown angle in equilibrium is important because it allows us to understand the forces acting on a system and how they are balanced. This information can be used to make predictions and solve problems related to the system.

How can the unknown angle in equilibrium be calculated?

The unknown angle in equilibrium can be calculated by using the principles of equilibrium, which state that the sum of all forces and torques acting on a system must be equal to zero. This can be represented mathematically using equations and solved to find the unknown angle.

What are some real-life examples of unknown angles in equilibrium?

Examples of unknown angles in equilibrium can be found in structures such as bridges and buildings, where the forces acting on them must be balanced for the structure to remain stable. Other examples include objects on an inclined plane or a pendulum at rest.

How does the unknown angle in equilibrium relate to other concepts in physics?

The concept of unknown angle in equilibrium is closely related to other principles in physics, such as Newton's laws of motion and the concept of torque. It also relates to the study of statics, which deals with the forces and torques acting on objects at rest. Understanding unknown angles in equilibrium is crucial in many areas of physics and engineering.

Similar threads

Calculate tilt angle of a bar lifted via two ropes on fixed points
Replies
7
Views
2K
Reactions of a redundant frame structure using Unit Load Method
Replies
11
Views
6K
Find Equilibrium: Solving a Uniform Bar Problem
Replies
6
Views
5K
Find force to raise load using friction and two bars
Replies
8
Views
5K
Statics: Mechanical Equilibrium
Replies
6
Views
8K
Three forces in Equilibrium. Find the angles.
Replies
2
Views
6K
Find the angle of a force by means of graphic solution
Replies
4
Views
2K
Pipeline structural Support loading case from riser pipeline.
Replies
2
Views
2K
Help with finding normal modes of a bar swinging on a string
Replies
4
Views
3K
Model Sling Load under Helicopter: Pendulum Dynamics
Replies
2
Views
4K

Hot Threads

Recent Insights

Back
Top