Finding Torque and Force for a Car w/ Two People

[aflowernamedu]

Torques and Forces?

I have found the first force,but I am not sure how to find the second :/.

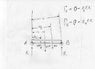
Two people sit in a car that weighs 8000N. The person in front weighs 700N, while the one in the back weighs 900N. Call L the distance between the front and back wheels. The person on the front is sitting L/3 back from the front wheels. The person on the back is sitting L/2 back from the PERSON ON THE FRONT. The car's center of gravity is a distance .400L behind the front wheels. How much force does each front wheel and each back wheel support if the people are seated alone the centerline of the car?

Ok so I did:
900 X 5/6L +700/3= F2
F2 =983
8000X .4L
3,200 L

3,200+983=4183
4183/2 = 2091/1000 = 2.09 KN

The book states the answers are 2.09 KN and 2.71 KN. How do I find 2.71??

 

[SteamKing]

For the car to be in static equilibrium, the sum of the reactions at the wheels must equal the weight of the car and the passengers. Simultaneously, the moment of the reactions and the weights about one set of wheels or the other must equal zero. If you write these equilibrium equations, they can be readily solved for the unknown reactions at the wheels.

 

[Spinnor]

What you did was to sum the torques about the front wheel to get the force on the back wheels. For the weight on the front wheels do you can sum the torques about the back wheel or you can just use the fact that the sum of the vertical forces is zero and at this point the only unknown vertical force is the force on the front tires, one equation in one unknown.