- #1
lichenguy
- 24
- 0
Homework Statement
A car accelerates from rest on a horizontal surface. The engine provides a
torque of τ = 200 Nm on each of the two front wheels. Each of the four
wheels on the car weigh m = 15 kg, have radius R = 0.35 m and can be
considered solid, uniform discs. The rest of the car (not the wheels) has a mass
of M = 1000 kg.
What is the acceleration of the car?
Homework Equations
I = 1/2mR2
τ = F*R
τ = I*α
a = α*R
The Attempt at a Solution
I can find the frictional force at one of the wheels:
Ff = τ/R
I can find the α of a wheel:
α = Ff*R/I
That means a = Ff*R2/I
Not much, but I'm not very good at this, really need help.
I don't know how to combine the body as well as the wheels. Anyone has some tips please? :D
Last edited:
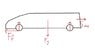
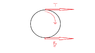
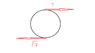
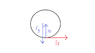
 . As a consequence, I had a factor of 2 where you have a factor of 6.
. As a consequence, I had a factor of 2 where you have a factor of 6. 