Josh1079
- 45
- 0
Hi,
I'm not sure about where I should post this question, so sorry in advance if I posted it in the wrong place.
My question is basically this screenshot. So I really have some difficulty in understanding the two equations. I mean how can it not be equal? I understand that rotations are non-commutative, but I really don't see why mathematically these two lines are not equal. Doesn't that violate the properties of matrix exponentials?
Thanks!
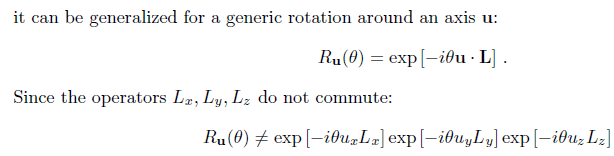
I'm not sure about where I should post this question, so sorry in advance if I posted it in the wrong place.
My question is basically this screenshot. So I really have some difficulty in understanding the two equations. I mean how can it not be equal? I understand that rotations are non-commutative, but I really don't see why mathematically these two lines are not equal. Doesn't that violate the properties of matrix exponentials?
Thanks!