Fluid Boundary layer in presence of a postive heat gradient

[Quentin_C]

I was wondering how a boundary layer would be dissipative of momentum if it was under the influence of a positive heat gradient.

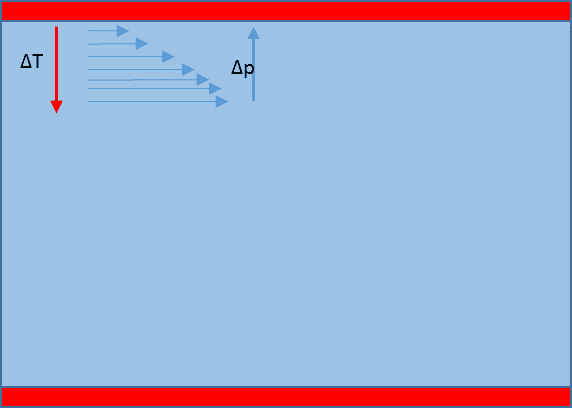
I understand that the reason that we don't see the boundary pressure equal the stagnation pressure is that the boundary is dissipative (so excess pressure above static pressure is "dumped" thru the pipe wall to the surroundings.)

If this heat gradient was reversed I could see that we would have an additional internal pressure gradient from a boundary quasi stagnation pressure to the lower static pressure in the moving fluid.

This gradient could be resolved by adding energy to the flowing fluid.

Should this mean that we would lose less momentum from the flow ?

 

[boneh3ad]

I am not 100% sure what you are asking here, but even in the presence of a heat flux into or out of the boundary layer (e.g. through the wall), the boundary layer is still dissipative. Even if you are adding energy into the flow to try to "decrease" your dissipation in the boundary layer, you still aren't actually decreasing it. Sure, you might measure less dissipation, but that is only because you are putting energy back into the flow to help make up for it, not because you are actually fundamentally changing the dissipation occurring in the system.