Fluid Mechanics - Pressure measurements

[CSUFStudent]

I'm having difficulty with one problem and was hoping someone could help me out. Here's the problem:

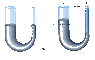
Mercury is poured into a U-tube as in Figure P14.18a. The left arm of the tube has a cross-sectional area A1 of 107.0 cm2, and the right arm has a cross-sectional area A2 of 4.10 cm2. One hundred grams of water are then poured into the right arm, as in Figure P14.18b.

(a) Determine the length of the water column in the right arm of the U-tube
(b) Given that the density of mercury is 13.6 g/cm3, what distance h does the mercury rise in the left arm?

I've attached the picture of the figure to this post

For part (a), given the radius of A2 and the volume of water, I easily got the length of the water column: 24.5cm

Part (b) is giving me a problem. How do I equate the change in height of the mercury due to the pressure of the water on it? I can determine the pressure of the water (P=F/A) on the mercury and thereby determine the upward pressure on the left arm (A2/A1=F2/F1). Once I get the change in height (dy) of the right arm I can use it to figure out the subsequent change on the left arm (A1/dy1=A2/dy2) but getting to that point is difficult for me.

I would greatly appreciate any suggestions or a point in the right direction.

Thanks!

 

[Clausius2]

Open the archive attached, I have modified the yours one a bit. Pay attention to the new references z, P_1, and L. P_1 is the pressure just at the interface water-mercury, and L is the length obtained in a).

Pressure at the interface (Hydrostatics):

P_1=P_{at}+\rho_w g L

that pressure is the same at the same height inside the mercury. So that, we can relate the jump of pressures at the left side:

P_1=P_{at}+\rho_{Hg} g (h+z)

So that:

\rho_w g L=\rho_{Hg} g (h+z) (1)

In addition and due to the mass conservation:

\rho_{Hg} z A_2=\rho_{Hg} h A_1 (2)

With (1) and (2) you can solve for h.

 

[CSUFStudent]

Thank you very much! The solution you provided worked perfectly. I don't think I would have ever come to the same conclusion on my own but with your explanation I understand the physics involved and how you arrived at the answer. Thanks again!