Calculating Flux Change and Meaning of Rotating Ring Diameter?

[dikmikkel]

Homework Statement

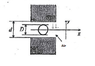
A ring can rotate about a horizontal axis(x), and a diameter placed on the x-axis. A uniform field is perpendicular to the ring -B0*y. The diameter of the ring is D. it spins with constant angular velocity ω around the x-axis. At at time t = 0 the ring is entirely in the xy plane

How do i find the flux change per time? And what does it mean that it can rotate around a diameter.
I've attached a figure.

Homework Equations

Flux = \int \vec{B}\cdot d\vec{a}

The Attempt at a Solution

At a time t = 0 the flux through the loop is 0 and i tried to write a solution using that B is constant:
Flux = B\int sin(\theta (t))d\vec{a}
Flux/dt = B\int cos(\theta(t) ) \omega d\vec{a}

 

[dikmikkel]

Nwm.
I found out.