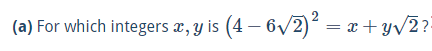danielw
- 5
- 0
Hi All
I have the following question.View attachment 5866
I have reviewed my notes but have not been able to crack this.
I tried two different ways, both wrong.
First:
$$
(4-6*\sqrt2)^2=$$
$$16-24*\sqrt2-24*\sqrt2+(36*2)
= 88-218*\sqrt2$$
so, $x=88$ and
$y=218$My second method was
$$(4-6*\sqrt2)^2= 4^2-(6*2)=28$$
but this is not in the form they want.
I'd really appreciate some advice on how to go about solving this kind of problem.
Thanks!
Daniel
I have the following question.View attachment 5866
I have reviewed my notes but have not been able to crack this.
I tried two different ways, both wrong.
First:
$$
(4-6*\sqrt2)^2=$$
$$16-24*\sqrt2-24*\sqrt2+(36*2)
= 88-218*\sqrt2$$
so, $x=88$ and
$y=218$My second method was
$$(4-6*\sqrt2)^2= 4^2-(6*2)=28$$
but this is not in the form they want.
I'd really appreciate some advice on how to go about solving this kind of problem.
Thanks!
Daniel
Attachments
Last edited by a moderator: