Oleg
- 9
- 0
Hello,
I'm currently doing the project and need to estimate the force that will act on the micron size superparamagnetic particle in the field of permanent magnet.
I found several article there similar problem is solved, but I a bit confused. I hope someone could hep me.
So, the main equation to start with is:
F = ∇(m⋅B),
where B the magnetic field and m - is the magnetic moment, which is also function of B (m = ƒ(B)).
If I have data how magnetic moment (or magnetization) depends on field, like this one:
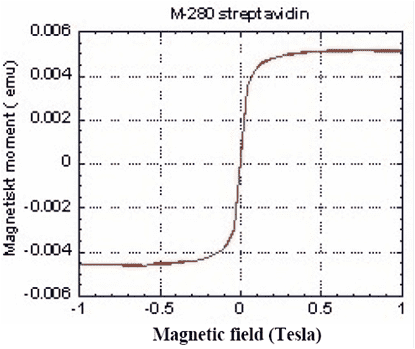
could I just use m as a constant for the given B? I so the equation terns to be:
F = m(∇⋅B).
Is it correct?
So next I need to to find ∇⋅B, which is as I understood is gradient of B (i.e. dBx/dx+dBy/dy+dBz/dz). Is it right? I have some doubts because in one article they use ∂Bx/dy term. I just thought that this difference may be due to difference in used magnets (permanent vs electromagnet).
And the last question is that would be direction of force vector? Anti-parallel to field?
I would appreciate your help.
Oleg
I'm currently doing the project and need to estimate the force that will act on the micron size superparamagnetic particle in the field of permanent magnet.
I found several article there similar problem is solved, but I a bit confused. I hope someone could hep me.
So, the main equation to start with is:
F = ∇(m⋅B),
where B the magnetic field and m - is the magnetic moment, which is also function of B (m = ƒ(B)).
If I have data how magnetic moment (or magnetization) depends on field, like this one:
could I just use m as a constant for the given B? I so the equation terns to be:
F = m(∇⋅B).
Is it correct?
So next I need to to find ∇⋅B, which is as I understood is gradient of B (i.e. dBx/dx+dBy/dy+dBz/dz). Is it right? I have some doubts because in one article they use ∂Bx/dy term. I just thought that this difference may be due to difference in used magnets (permanent vs electromagnet).
And the last question is that would be direction of force vector? Anti-parallel to field?
I would appreciate your help.
Oleg
