I Force applied to a sphere off center of mass

[Hamza Qayyum]

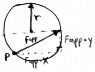
I'm trying to model a sphere having force applied at position P in the following diagram:

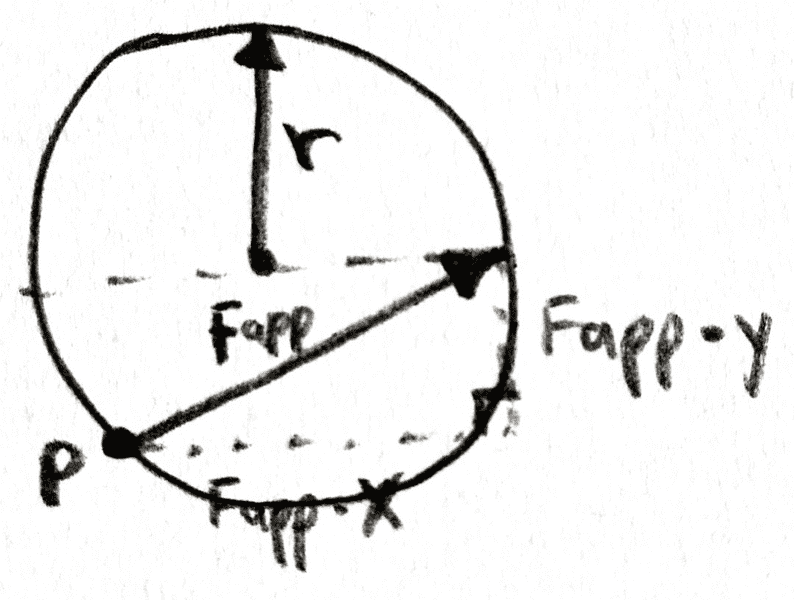
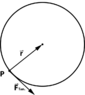
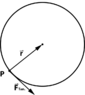
I know that this applied force will have an x and y component; the y component will propel it upwards, but what I am confused about is the x component of the force. I know that the x component will propel it forwards (linear velocity) and make it spin (angular velocity). I can calculate the rotational force as follows:F_{rot.}=ma_{tangential}F_{rot.}=mr\alpha=\frac{mr\omega}{\Delta t}However, what I don't know is the proportion of F_{app.\,x} that contributes to the rotational force and the proportion that contributes to linear force in the x direction. It doesn't make sense if I try to think of both being proportional. That would only work if the sphere were rolling on the floor without slipping, in which case V_{Center\,of\,mass}=r\omega.

Any ideas on the topic would be greatly appreciated. Maybe I'm missing something crucial, as I'm still a high school student, with most of this rotational dynamics stuff being self learned. Thank you.

 

[FactChecker]

You don't divide up the force to calculate the linear acceleration at the CG. F=mA works at the center of mass regardless of where the force is applied. The rotational acceleration is calculated separately as the result of the lever arm and the force component perpendicular to it.
The following figure is a simple case that hopefully will give you some intuition of why the linear acceleration at the CG will be the same regardless of where the force is applied. The rotation is a result of the side where force is applied accelerating faster than the other side.

 

[Hamza Qayyum]

You don't divide up the force to calculate the linear acceleration at the CG. F=mA works at the center of mass regardless of where the force is applied. The rotational acceleration is calculated separately as the result of the lever arm and the force component perpendicular to it.
The following figure is a simple case that hopefully will give you some intuition of why the linear acceleration at the CG will be the same regardless of where the force is applied. The rotation is a result of the side where force is applied accelerating faster than the other side.

View attachment 220182

Thank you for the diagram; your answer made things clearer. Please let me know if I am understanding you correctly in terms of calculating the angular acceleration; you're proposing that tangent to point P, there is a force, and combined with the radius of the circle, it produces a torque:

\vec{\tau}=\vec{r} \times \vec{F_{Tan.}}||\tau||=||r||\cdot||F_{Tan.}||\sin{\theta}\tau=r\cdot ma_{Tan.}=m r^2 \alpha=I\alphaI do understand this part, but what I am still confused about is how to deduce \vec{F_{Tan.}} from \vec{F_{app}} in the first place? I also understand the first part of your answer, that the translational acceleration is simply:||\vec{a_{Trans.}}||=\frac{||\vec{F_{app}}||}{m}But I do not understand the latter, of how \vec{F_{Tan.}} derives from \vec{F_{app}}.

 

[A.T.]

But I do not understand the latter, of how \vec{F_{Tan.}} derives from \vec{F_{app}}.

There is nothing to derive. You can plug your applied vorce directily into the vetor forumla:
\vec{\tau}=\vec{r} \times \vec{F_{app.}}
The cross product makes sure that only the tangential component matters.

 

[FactChecker]

The only thing I see to comment on is that you should look harder at the cross product of vectors, how to calculate it, and how easily it gives you the complete answer in vector form. You are using the norm and dot product where it makes the statement weaker than necessary or maybe even wrong. For example:

\tau=r\cdot ma_{Tan.}=m r^2 \alpha=I\alpha

I'm not sure what you mean here. If this is a vector statement then it is wrong. I see you dropped the norms but did not add vector symbols.

||\vec{a_{Trans.}}||=\frac{||\vec{F_{app}}||}{m}

There is no need for the vector norms here. This is true as a vector statement -- both direction and magnitude.

Other than these comments, I think you are correct.

PS. I really like the clarity and attention to detail of your work here. So many people with a lot more years of experience (including maybe myself) are relatively sloppy in how they present their thoughts.

 

[A.T.]

\vec{\tau}=\vec{r} \times \vec{F_{Tan.}}

Just noticed that you have the r vector pointing the wrong way in your diagram. See:
https://en.wikipedia.org/wiki/Torque#Definition_and_relation_to_angular_momentum

Here you just plug F itself into the formula:
\vec{\tau}=\vec{r} \times \vec{F}
You don't have to compute the perpendicular component first.

 

[Hamza Qayyum]

There is nothing to derive. You can plug your applied vorce directily into the vetor forumla:
\vec{\tau}=\vec{r} \times \vec{F_{app.}}
The cross product makes sure that only the tangential component matters.

Ah, I see. Thank you for clarifying that.

I'm not sure what you mean here. If this is a vector statement then it is wrong. I see you dropped the norms but did not add vector symbols.There is no need for the vector norms here. This is true as a vector statement -- both direction and magnitude.

Sorry, got a bit sloppy there. In vector form, I think this is the correct statement:
\vec{\tau}=\vec{r}\times\vec{F_{Tan.}}=\vec{r}\times m\vec{a_{Tan.}}\vec{v_{Tan.}}=\vec{\omega}\times\vec{r}\Rightarrow\vec{a_{Tan.}}=\vec{\alpha}\times\vec{r}\vec{\tau}=\vec{r}\times m(\vec{\alpha}\times\vec{r})\vec{\tau}=m\Big[\vec{r}\times(\vec{\alpha}\times\vec{r})\Big]\vec{\tau}=m\Big[(\vec{r}\cdot\vec{r})\vec{\alpha}-(\vec{r}\cdot\vec{\alpha})\vec{r}\Big]\vec{\tau}=m\Big[||\vec{r}||^2 \vec{\alpha}-(\vec{r}\cdot\vec{\alpha})\vec{r}\Big]Also, thanks for the compliment; glad I haven't pissed off anyone early on here haha

Just noticed that you have the r vector pointing the wrong way in your diagram. See:
https://en.wikipedia.org/wiki/Torque#Definition_and_relation_to_angular_momentum
View attachment 220207
Here you just plug F itself into the formula:
\vec{\tau}=\vec{r} \times \vec{F}
You don't have to compute the perpendicular component first.

Ah, yes, that is a mistake. Thank you for picking that out.