opus
Gold Member
- 717
- 131
Homework Statement
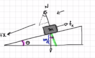
This is more of a general question, not specific to any problem. I am not too good at drawing force diagrams so I was hoping I could post an image and get some guidance on how to find the forces acting on the object.
In this case, we have a block sliding down a plane of angle θ and a coefficient of kinetic friction μ.
My troubles usually lie with breaking the normal force and gravitation force down to components that are acting along the plane. Here I have made the plane the x axis, with down the plane being positive.
To me it seems as the component of the normal force acting along the plan should be ##mgcos(\theta)##. ##f_k## will I believe be μN (not any particular component of N, but just N). I am unsure of the gravitational component though.
Please see my attached image. Thank you.