Force F on Mass m at Angle Θ: Acceleration Calculations

[dreamz25]

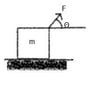
q) A force F acts on a block of mass m placed on a horizontal smooth surface at an angle Θ with horizontal. Then

(A) If F sinΘ < mg then a = (F + mg) / m

(B) Acceleration = FcosΘ/m where, F > mg cosecΘ

(C) Acceleration = F/m if FsinΘ > mg

(D) If F SinΘ > mg then a = (F + mg) / m

my work
--------

on drawing the F.B.D we we get..

clearly there will be linear and vertical acceleration as well...
Now if F sinΘ > mg then the Normal force will be 0
=> F sinΘ - mg = ma_y ---- (i)

and, F cosΘ = ma_x ------ (ii)

Adding the two eqns. we get,

F sinΘ + F cosΘ - mg = m (a_x + a_y)

or, a_x + a_y = (F - mg) / m

but the correct option is d.

couldn't represent vectors with their notations so please understand
it urselves.

Am i wrong? if yes then where and why?

Thanks in advance...!

 

[Doc Al]

None of those answers look right. Are you sure there's not a typo in there? (Check the orientation of the > signs.)

And you can't just add perpendicular vector components, such as a_x + a_y.

 

[dreamz25]

why not...?

 

[Doc Al]

why not...?

They are vectors. Direction counts.