- #1
mattlfang
- 28
- 8
- Homework Statement
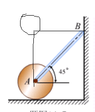
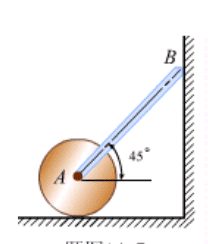
- Stick with mass m leans on the wall on B end. A end hinges on the center of the cylinder with mass M and radius r. Initial position has angle of 45 degrees. No friction on the wall or the hinges. Cylinder starts rolling from initial position, but the frictional force on the cylinder can be ignored. What's the acceleration of A point at the initial position
- Relevant Equations
- Decomposition of forces. Newtonian second law.
So the acceleration of point A was given by a force F exerted on cylinder that's along the direction of the stick, decomposed into the horizontal direction. so aA = F cos Θ
The same force along the opposite direction is exerted on stick, and if we decompose that in vertical and horizontal direct, we can compute the acceleration of the stick m. so aStick = (F cos Θ - mg) / m
The acceleration of the stick and the cylinder satisfies certain geometric relation, then we can probably compute the force and the acceleration.
But I struggle to finish the last part off.
this is the answer. but I have no solutions.
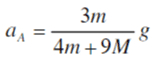
The same force along the opposite direction is exerted on stick, and if we decompose that in vertical and horizontal direct, we can compute the acceleration of the stick m. so aStick = (F cos Θ - mg) / m
The acceleration of the stick and the cylinder satisfies certain geometric relation, then we can probably compute the force and the acceleration.
But I struggle to finish the last part off.
this is the answer. but I have no solutions.
Last edited: