Force from a Current in an Infinite Wire on a Square Wire Loop Nearby

[Schfra]

Homework Statement

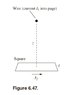
Figure 6.47 shows a horizontal infinite straight wire with current I1 pointing into the page, passing a height z above a square horizontal loop with side length l and current I2. Two of the sides of the square are parallel to the wire. As with a circular ring, this square produces a magnetic field that points upward on its axis. The field fans out away from the axis. From the right-hand rule, you can show that the magnetic force on the straight wire points to the right. By Newton’s third law, the magnetic force on the square must therefore point to the left.
Your tasks: explain qualitatively, by drawing the fields and
forces, why the force on the square does indeed point to the left;
then show that the net force equals μ0I1I2l2/2πR2, where R =
z2 + (l/2)2 is the distance from the wire to the right and left sides of the square. (The calculation of the force on the wire is a bit more involved. We’ll save that for Exercise 11.20, after we’ve discussed magnetic dipoles.)

Homework Equations

B = uI/(2piR)

The Attempt at a Solution

I’m not quite sure where to start on this one. The first part of the question is a bit confusing, what do they want me to do? It seems like they already explained why the force on the square points left. Should I just draw a picture of what they already explained?

 

[TSny]

They used Newton's 3rd law to conclude that the force on the loop is to the left. But they want you to verify this by analyzing the magnetic force on various parts of the loop to show that the net magnetic force on the loop is to the left (without using the 3rd law).

Your expression for the force is μ0I1I2l2/2πR2. It would be helpful if you used the subscript and superscript tools on the toolbar to write this more legibly.

 

[Schfra]

They used Newton's 3rd law to conclude that the force on the loop is to the left. But they want you to verify this by analyzing the magnetic force on various parts of the loop to show that the net magnetic force on the loop is to the left (without using the 3rd law).

Your expression for the force is μ0I1I2l2/2πR2. It would be helpful if you used the subscript and superscript tools on the toolbar to write this more legibly.
View attachment 223748

Sorry, that force is μ₀I₁I₂L²/2πR².

How do I know how the magnetic field affects the square? I’m only familiar with finding the effects of magnetic fields on moving charges.

 

[TSny]

Sorry, that force is μ₀I₁I₂L²/2πR².

How do I know how the magnetic field affects the square? I’m only familiar with finding the effects of magnetic fields on moving charges.

So, you haven't covered the formula for the magnetic force on a straight piece of wire that carries a current?

http://www.sparknotes.com/testprep/books/sat2/physics/chapter15section3.rhtml

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html

 

[Schfra]

So, you haven't covered the formula for the magnetic force on a straight piece of wire that carries a current?

http://www.sparknotes.com/testprep/books/sat2/physics/chapter15section3.rhtml

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/forwir2.html

But that formula doesn’t tell us about how the square reacts to the magnetic field from the wire does it? And isn’t the force acting on the square what I need to find?

 

[TSny]

But that formula doesn’t tell us about how the square reacts to the magnetic field from the wire does it? And isn’t the force acting on the square what I need to find?

Yes, you need to find the force on the square. The wire that carries a current $I_1$ produces a magnetic field around it. The square loop sits in this magnetic field. So, this magnetic field will exert a magnetic force on the current in the loop. You might start with the left side of the loop (where the current is coming out toward you) and think qualitatively (right-hand-rule) about the direction of the magnetic force on this side of the loop. You will need to think about the direction of the magnetic field (producued by $I_1$) at this side of the loop.