Discussion Overview
The discussion revolves around the forces exerted on the walls of a pressurized tank as water enters, particularly focusing on the dynamics of air compression and the resulting pressure differentials. Participants explore theoretical models and equations related to fluid dynamics and pressure changes in a rigid tank without a relief valve.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
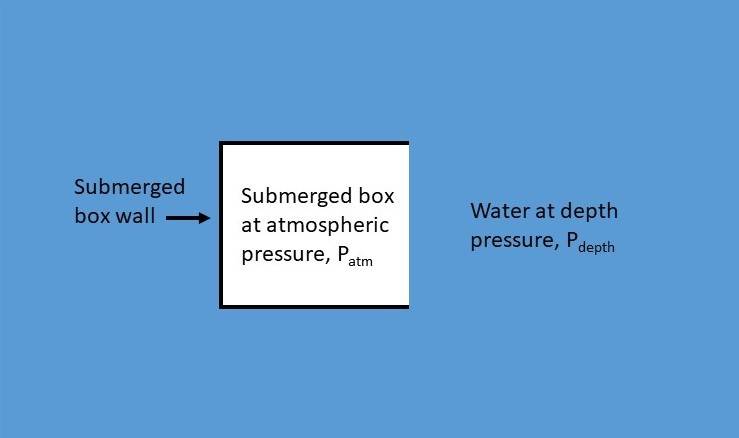
- One participant proposes a force equation based on jet discharge propulsion, suggesting that the force can be expressed as $$ F = 2 A \left( P_{depth} - P_{atm} \right) $$ but questions how to incorporate the inward rushing water that compresses the air.
- Another participant seeks clarification on the definitions of variables and the reasoning behind the factor of 2 in the proposed equation.
- A participant explains that initially there is no compressed air, but as water enters, atmospheric air becomes compressed, and the area considered is the wall area.
- One participant describes a hypothetical scenario involving a submarine to illustrate the dynamics of pressure waves and the effects of a sudden opening in a wall, emphasizing the rapid acceleration of water and air compression.
- Another participant notes that as the pressure differential decreases, the infiltration of water will slow down, and the water level will eventually cover the orifice, introducing aerodynamic drag from the air.
- Some participants discuss the potential for numerical modeling to calculate remaining air volume, instant pressure, and temperature, providing equations for these calculations.
- One participant expresses surprise at the drag force from air counteracting the propulsive force from hydrostatic pressure.
Areas of Agreement / Disagreement
Participants express various viewpoints and hypotheses regarding the dynamics of the system, with no clear consensus reached on the correct approach or outcomes. Disagreements exist regarding the application of proposed equations and the implications of different scenarios.
Contextual Notes
Limitations include assumptions about the rigidity of walls, the nature of the pressure differential, and the effects of drag forces, which remain unresolved in the discussion.
 !
!