Force needed to push an incline with a mass on it

[nagaromo]

Homework Statement

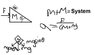
Incline with the mass of M and angle of theta. mass on the incline with the mass of m. Find the force needed to push the entire system such that the mass remains at rest relative to the incline. Everything is frictionless

Homework Equations

F=ma

The Attempt at a Solution

well my teacher has gone over the problem where a=F/(M+m) but after that, I was completely lost and we arrived with the answer of F=(m+M)gtan\theta

I'll love you if you could please explain to me how to arrive to that answer! <33 THANK YOUU

 

[xsweetox]

1. draw an FBD for m on a tilted axis x prime and y prime.
2. convert that FBD to a normal axis by splitting the force arrows into components.
3. draw an FBD for M.

1. first, you need to draw all the force arrows. You got part of the forces right in your diagram. There is Fgsin(theta) and Fg(costheta). Don't forget, there is also a normal force acting on the block perpendicular to the incline. Also, The reason why the block does not slide down the ramp is because M exerts a force F(Mm) on it. Therefore, it points in the opposite direction of Fgsin(theta).

2. Next, you need to break up all these slanted force arrows into their x and y normal axis directions. after this, you will notice that the net force in the positive y direction is F(Mm)sin(theta) - Fncos(theta). This is equal to the net force in the negative y direction, Fg, as the block does not accelerate in the y direction. The net force in the positive x direction is Fgsin(theta)cos(theta). in the opposite direction you have F(Mm)cos(theta). Fgsin(theta)cos(theta) is bigger because the block does accelerate in the x direction.

3. now you draw an FBD for M. The net force in the positive x direction is Fa, the applied force. there is a force that m exerts on M, which is slanted toward the bottom left corner. When you break up this force into the x and y perpendicular forces, you get the following: a force pointing in the negative x direction F(mM)cos(theta); a force pointing in the negative y direction F(mM)sin(theta). On top of this, you have a normal force and a force of gravity acting in opposite directions. They are not equal! Fn = Fg + F(mM)sin(theta).

the acceleration of M is equal to the acceleration of m.

am = Fnet m
= Fgsin(theta)cos(theta) - F(Mm)cos(theta)

aM = Fnet m
= Fa - F(mM)cos(theta)

F(mM) = F(Mm) (Newton's third law)

then you use the equations to solve for a.

btw, i used components and not vectors. hope this helps.

 

[xsweetox]

oops, aM= Fnet M

 

[nagaromo]

thank you! :D