Force on a Nail: Solving with Trig & Forces

  • Thread starter e4physics
  • Start date
  • Tags
    Force
In summary, Force is a physical quantity that is defined as the push or pull that an object experiences due to its interaction with another object. It is measured using the unit Newton (N), and trigonometric functions can be used to calculate its components in different directions. In solving problems involving a nail, force plays a crucial role, and we can use trigonometry and force equations to accurately determine its effect and stability.
  • #1
e4physics
6
0
Hi I am trying to solve this question in my book but i am not getting the write answer , can some one explain this.

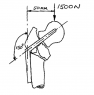
Question : The approximate force which would tend to impact the proximal fragment on the nail and distal fragment in the diagram above is ---------- NEWTONS?

I tried to solve this question using simple trigonometry and resolution of forces but could not get the answer. The question is asking for the forces in the nail.



THE DIAGRAM IS ATTACHED
 

Attachments

  • LM0304.png
    LM0304.png
    16.3 KB · Views: 420
Physics news on Phys.org
  • #2
You should follow the HW template and at least show your work.
 

FAQ: Force on a Nail: Solving with Trig & Forces

What is the definition of force?

Force is a physical quantity that is defined as the push or pull that an object experiences due to its interaction with another object.

How is force measured?

Force is measured using a unit called Newton (N), which is equivalent to 1 kilogram meter per second squared (kg*m/s^2).

How does the trigonometric function relate to force?

Trigonometric functions, such as sine, cosine, and tangent, can be used to calculate the components of a force vector in different directions. This allows us to break down a force into its horizontal and vertical components, making it easier to solve problems involving forces on an object.

What is the role of force in solving problems involving a nail?

Force is a crucial factor in solving problems involving a nail. The force applied on a nail, along with its direction and magnitude, determines whether the nail will stay in place or move. By using trigonometric functions and force equations, we can accurately determine the force on a nail and its effect on its surroundings.

How can we apply trigonometry and forces to solve problems involving a nail?

To solve problems involving a nail, we can use the principles of trigonometry and forces to break down the force acting on the nail into its components and then use equations such as Newton's Second Law and the Pythagorean Theorem to calculate the force on the nail. We can also use these concepts to determine the stability of the nail and predict its behavior under different conditions.

Similar threads

Force on rectangular loop by a current in a long straight wire
Replies
4
Views
744
Potential Mistake in Free-Body Diagram
Replies
5
Views
1K
Correct approach in resolving a force into its different components
Replies
4
Views
1K
Force on a charge from a nearby charged rod
Replies
2
Views
584
Questions Regarding a Cat Going Up a Ramp
2
Replies
56
Views
3K
Finding the angle that a string makes with a wall and its tension
Replies
4
Views
1K
How to find the forces in a particular framework of light rods
Replies
11
Views
2K
Finding the weight of an object submerged in water
Replies
17
Views
3K
Torque On a Clock Hanging from a Nail
Replies
4
Views
3K
Block and pulley on movable incline
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top