Force to raise a cylinder over an edge

[Karol]

Homework Statement

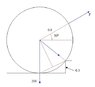
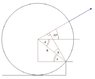
The cylinder with mass 200[kg] and radius 0.8[m] tries to climb a 0.3[m] high edge with a force F exerted at an angle of 30⁰. what's the force and what's the minimum force for the cylinder to climb

Homework Equations

Moments: F₁L₁=F₂L₂

The Attempt at a Solution

The weight balances the the force, i made moments around the edge and got a true answer F=1670[N], but i don't understand the second question, about the minimum force, and it's about 766[N]

 

[mfb]

"Minimal force" might mean the force needed if the angle can be adjusted. But then the two values should not be so different. Maybe you can adjust the point where it acts on as well. If that is the full problem statement and 766 N is the given answer, it is poorly written.

 

[haruspex]

"Minimal force" might mean the force needed if the angle can be adjusted. But then the two values should not be so different. Maybe you can adjust the point where it acts on as well. If that is the full problem statement and 766 N is the given answer, it is poorly written.

To get an answer so much lower, it must be allowed to apply the force further from the step.

 

[TSny]

Maybe you can adjust the point where it acts on as well.

To get an answer so much lower, it must be allowed to apply the force further from the step.

Ah! Yes. That's how you can get about 766 N.

 

[Satvik Pandey]

Hi Karol.

I consider that the ball pivots about point of contact (O). So the CoM of the ball will perform circular motion about point O.

Now - work energy theorem states that 'Work done by all the forces on the system is equal to the change in the kinetic energy'.
As the required force is minimum so the ball the velocity of the CoM of the ball at the final position (i.e when the CoM is just above the point O) should be zero.

Now there are three force acting on the ball -- gravity, F and Normal force (N). Work done by N is zero.

Work done by F=work done by mg...(1)

Work done by mg can be find easily.

The black curve shows the trajectory of the CoM. Angle $\phi$ can be found easily. Let the Com be at any arbitrary position such that it has rotated by angle $\theta$ about O.

Work done by F is $\int _{ 0 }^{ (90-\phi ) }{ FRcos(30-(\theta +\phi ))d\theta }$.

Just put the value in eq. (1). I think you will get the answers.

 

[Karol]

Work is either torque times angular displacement of force times displacement and in both ways i get an other equation than: $\int _{ 0 }^{ (90-\phi ) }{ FRcos(\theta +\phi )d\theta }$
According to the new drawing, for the initial position: α=90-(30+Φ) so W=FR cos[90-(30+Φ)]
Of course we add θ for an arbitrary position and take an integral at the same boundaries

 

[Satvik Pandey]

Work is either torque times angular displacement of force times displacement and in both ways i get an other equation than: $\int _{ 0 }^{ (90-\phi ) }{ FRcos(\theta +\phi )d\theta }$
According to the new drawing, for the initial position: α=90-(30+Φ) so W=FR cos[90-(30+Φ)]
Of course we add θ for an arbitrary position and take an integral at the same boundaries

I made a mistake in #post 5.
The work done by F is $\int _{ 0 }^{ (90-\phi ) }{ FRcos((\theta +\phi)-60 )d\theta }$

If you consider the AO as the initial condition and BO as the final condition you will find that initially $\theta=0$ and final $\theta=90-\phi$.

What would you get after evaluating the integral?

 

[mfb]

@Satvik Pandey: That does not work. What you calculate would be the average force needed, but the force depends on the angle, so you underestimate the force needed to start the lifting process.

 

[Karol]

The geometry i have drawn is to scale, the force is above the tangent, at the initial position A and further, not like you drew, so the integral is:
$$W=\int_0^{51.32} F\cdot 0.8 \cdot \cos (60-\phi)d\phi=-0.8F\cdot\sin(60-\phi)\vert^{51.32}_0=-0.8F(\sin 8.68-\sin 60)=0.57F$$
The gain in potential enrgy equals W: $0.57F=2000[N]\cdot 0.3[m]\rightarrow F=1053$
But that is only theoretical since it's smaller than the force needed to lift it at the beginning

 

[haruspex]

The geometry i have drawn is to scale, the force is above the tangent, at the initial position A and further, not like you drew, so the integral is:
$$W=\int_0^{51.32} F\cdot 0.8 \cdot \cos (60-\phi)d\phi=-0.8F\cdot\sin(60-\phi)\vert^{51.32}_0=-0.8F(\sin 8.68-\sin 60)=0.57F$$
The gain in potential enrgy equals W: $0.57F=2000[N]\cdot 0.3[m]\rightarrow F=1053$
But that is only theoretical since it's smaller than the force needed to lift it at the beginning

As mfb has pointed out, it is not only unnecessary to consider energy or perform integrals to answer this question, it will give the wrong answer.
All you have to do is figure out where and at what angle to apply the force to get the cylinder moving. Beyond that, you could consider whether a larger force may be required at some later point in lifting it over the step (if the direction and point of application are not allowed to change?).

 

[Satvik Pandey]

@Satvik Pandey: That does not work. What you calculate would be the average force needed, but the force depends on the angle, so you underestimate the force needed to start the lifting process.

Thank you mfb for pointing it. Sorry Karol, I lead you on the wrong path.:s