cookiemnstr510510
- 162
- 14
Homework Statement
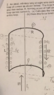
An ideal, infinitely long straight wire carries a current I1 and is partially surrounded by a loop of current as shown below (image attached). The loop has length L, parallel to the infinitely long wire. The loop carries current I2.
A) Calculate the magnitude and direction of the force exerted on the entire loop.
B) Does this force tend to cause rotation of the loop?
Homework Equations
Fwire=ILxB= ILBsinθ (The F, L, and B are all vectors, once you do the cross product they are no longer vectors)
The Attempt at a Solution
A)
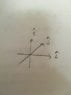
Each wire is creating its own magnetic field at the location of the other wire. I broke the semicircular curved wire into 4 segments, labeled them a-d (segments.jpg).
The magnetic field from the infinitely long wire on segment "a" and "c" of the curved semicircular wire loop is everywhere parallel or anti parallel to the current traveling through those segments. Therefore the force on those wires is zero. The only segments that are affected by the infinitely long wire are segments "b" and "d" of our loop. Segment "b" feels a force towards the center of its circular shape (to the right) and segment "d" feels a force to the right.
Fwire d=I1LxB1=I1LB1(i hat direction)
Fwire b=I1LxB1=I1LB1(i hat direction)
So the force exerted on the entire loop is
2[I1LB1(i hat direction)]
B) Not sure how to approach part b, any advice?
Thanks in advanced! As always I appreciate the help!
Attachments
Last edited by a moderator: