- #1
umby
- 50
- 8
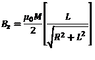
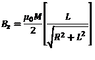
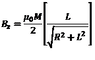
Hi, I am looking for the formula of the magneti field along the axis of a axially magnetized cylindrical magnet.
Unfortunately, there are quite different answers on Internet.
Is the uploaded formula (where R is the magnet radius and L its length) correct?
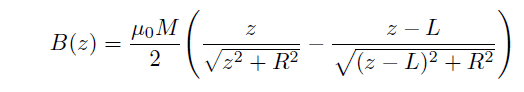
Unfortunately, there are quite different answers on Internet.
Is the uploaded formula (where R is the magnet radius and L its length) correct?