Formula for torque on a coil in a magnetic field

[Alettix]

Hi!
I have some simple questions on the formula for torque on a coil in a magnetic field, ie this one:

τ = NIA sinθ

where I is the current flowing through the coil, A is the area of one loop, N is the number of loops, B is the magnitude of the magnetic field and θ is the angle between the vector normal to the coil's plane and the magnetic field vector.

All the derivations I have seen to this formula begin with a quadratic single loop, and then in the last step it is said that the derived results apply to coils with N loops of arbitrary geometry.

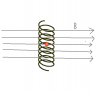
My questions are: Is the formula still applyable if we have a long solenoid (as in the picture)? Why/ Why not?
If it is applyable: Is it obvious that the torque is around the middle of the solenoid?
If its'nt: Is there any other formula for magnetic torque on a solenoid? Or do you have any suggestion how I could derive one?

Thank you very much! :)

 

[saurabh tiwari]

Same formula i.e. NIABsinθ is applicable

 

[Orodruin]

If it is applyable: Is it obvious that the torque is around the middle of the solenoid?

In the absence of an overall force, it does not matter which point you compute the torque with respect to.

A difference to a single loop when you have an extended solenoid is that there will be a net force due to the current flowing slightly in the axial direction as well.

 

[saurabh tiwari]

In the absence of an overall force, it does not matter which point you compute the torque with respect to.

A difference to a single loop when you have an extended solenoid is that there will be a net force due to the current flowing slightly in the axial direction as well.

Can you please explain why there is net force on solenoid

 

[Orodruin]

Can you please explain why there is net force on solenoid

This is described in my previous post. There is a net current flowing vertically in the image (up or down depending on current direction). This gives a net force perpendicular to the image.

If the solenoid is short, the forces involved in producing the torque are much larger than this force, but if it is long (i.e., the winding angle large) the forces producing the torque and the net force will be comparable. In the limiting case when you do not wind the wire around, the force is all that remains.

 

[saurabh tiwari]

As per my knowledge solenoid is defined as tightly wounded turns so vertical currents shouldn't be significant

 

[Orodruin]

As per my knowledge solenoid is defined as tightly wounded turns so vertical currents shouldn't be significant

You will always have a vertical current, simply from the fact that you are letting current enter at the bottom and get out at the top (or vice versa). This will unambiguously lead to a net force. It will typically be relevant mainly for force balance, but also in terms of realising that the torque is not equal for all points in the system (although, since the force is typically small relative to the torque produced by the winding, changes in the torque for points within the solenoid may be negligible).

 

[rude man]

This is EDITed from a while ago, did not want to look stupid!

Each turn will have a torque applied about a cross-sectional diameter perpendicular to the B direction, just as though it were a flat single-turn coil.
In addition, there is a force along the direction perpendicular to B and the solenoid axis. This force is proportional to arc length everywhere along a circumference so does not produce any torques.
The foregoing assumes a long solenoid.

You can use the equations for a helix to come up with numbers. Those, parametrized, can be
x = R cosθ
y = R sinθ
z = cθ
so that interwinding spacing = 2πc.
You can show dF = I B(j c - k R cosθ) dθ with B = i B.
I = current
vectors in bold.

 

[Alettix]

Firstly, Thank you all for your answeres! :)

There is no torque applied about the center as you have shown.
Each turn will have a torque applied about a cross-sectional diameter perpendicular to the B direction, just as though it were a flat single-turn coil.

Can the torque's on each turn not be summed up to produce a net torque about the center I marked in the picture? So the coil will not start to rotate if we lead a current through it in a magnetic field? I thought it did.

The foregoing assumes a long solenoid.

You can use the equations for a helix to come up with numbers. Those, parametrized, can be
x = R cosθ
y = R sinθ
z = cθ
so that interwinding spacing = 2πc.
You can show dF = I B(j c - k R cosθ) dθ with B = i B.
I = current
vectors in bold.
The torque magnitude about the aforesaid diameter calculates to 4R² I B.

Note aside:
Interestingly, this is not the same torque as that computed when considering a single-turn coil of area
A = πR² as having magnetic moment
μ = I A so torque = μ B = πR² I B
which differs by a ratio of π/4 = 0.785. Anybody want to comment on the discrepancy? I can submit math details. For a square coil the answers are the same but seemingly not for a round coil.

This was very interesting! Have you maybe got a link to the math details (or know where I could find them)?

 

[Orodruin]

Simple application of the right-hand rule will tell you that there is a torque about the center in the direction perpendicular to the image. The force in the axial direction is directed in different directions on different sides of the solenoid as given here:

You can show dF = I B(j c - k R cosθ) dθ with B = i B.

The k R cosθ will appear in a cross product with i R cosθ from the position vector, resulting in a cos^2(θ) term which does not integrate to zero.

 

[rude man]

@ orodruin: Simple application of the right-hand rule will tell you that there is a torque about the center in the direction perpendicular to the image. The force in the axial direction is directed in different directions on different sides of the solenoid as given here:

The k R cosθ will appear in a cross product with i R cosθ from the position vector, resulting in a cos^2(θ) term which does not integrate to zero.[/QUOTE]
Agreed. I didn't realize that, for each winding, the torque about (my) y axis, the one out of the drawing, would rotate the entire solenoid about an axis parallel to that axis.

I had previously found my factor-of-two mistake in giving the torque magnitude.
Thanks for your help.

@Alettix: I can send you the missing steps in the equations if you're still interested.
rm.

 

[Alettix]

Hello again!

Sorry for the late answer, thank you all for your help! Yes @rude man , I'm still interested in the math details if it's not a problem to send them over. :)

Just to make sure I have not missunderstod anything; we have come to the conclusion that there is a net torque around the center of the coil and that this torque rotates it in the plane of the drawing?

 

[Orodruin]

we have come to the conclusion that there is a net torque around the center of the coil and that this torque rotates it in the plane of the drawing?

Correct. There will also be a net force perpendicular to the drawing. The point of application of the resultant force is also the centre of the coil and this may give you an additional torque if you consider another point. The additional torque will generally be small around any point within the coil as long as there is a fair number of windings in the coil.

 

[Alettix]

Correct. There will also be a net force perpendicular to the drawing. The point of application of the resultant force is also the centre of the coil and this may give you an additional torque if you consider another point. The additional torque will generally be small around any point within the coil as long as there is a fair number of windings in the coil.

Thank you so much for the clarification!

 

[rude man]

Hello again!

Sorry for the late answer, thank you all for your help! Yes @rude man , I'm still interested in the math details if it's not a problem to send them over. :)

Just to make sure I have not misunderstod anything; we have come to the conclusion that there is a net torque around the center of the coil and that this torque rotates it in the plane of the drawing?

I have to admit, I can't see the second torque orodruin describes. The force pointing into/out of the page is pulling every tiny section of the entire coil in that same direction, and I don't see any net moment arm to generate net torque unless the turns spacing is non-uniform. Perhaps he will explain further.

 

[Orodruin]

I'll send you the math separately via private message.
I have to admit, I can't see the second torque orodruin describes. The force pointing into/out of the page is pulling every tiny section of the entire coil in that same direction, and I don't see any net moment arm to generate net torque unless the turns spacing is non-uniform. Perhaps he will explain further.

As I said, it provides no net torque about the center of the coil, just a net force. If you consider any point other than the center (or rather, other than the axis pointing out of the image through the center), this force will produce a net torque.

 

[rude man]

@Alettix, I decided to post the math here. I got you confused with another OP with whom I've had some private chat.
So, going back to my post 8, consider a vector element of wire ds = i dx + j dy + k dz
i j k unit vectors; all vectors in bold.
The force on this element is dF = I ds x B where B = i B.
The solenoid axis is the z axis (k direction) and the y-axis (j direction) points into or out of the page (depending on direction of I).
You should perform this multiplication to see that dF = I B (j c - k R cosθ).
From this you see that there is a constant force on every element of ds = I B c in the j direction, but this is uniformly distributed around the entire solenoid & thus produces no rotation anywhere (that I can see. The torque orodruin describes would seem to be about any axis parallel to, but away from, the x-axis (x axis passes thru the center) but any rotation about such an axis would move the c.g. in a forbidden direction (k) by Newton). Maybe I'm still not seeing this part right).
At this point I suggest you draw a circle representing one winding's projection on the x-y plane. The differential torque about the y-axis will be the force dF times the lever-arm which is a straight line perpendicular to the y-axis and going to each ds element along the circle. You can see that this arm has length R cosθ. So the total torque per winding about the y-axis is df*Rcosθ integrated from θ = 0 to θ = π/2 and then *4 for all 4 quadrants (see why this is right?). You wind up with torque = π I B R² for each winding. You need to do this math yourself. So the effect is to rotate the entire solenoid about an axis parallel to the y axis. From what I said above (Newton) you might try to think about why the rotation is about the y-axis itself and not some axis parallel to, but away from, the y axis, like about the bottom or top of the solenoid.

 

[rude man]

@Alettix, a couple more observations if you're not sick of this by now!

1. The solenoid acts just like a bar magnet in the B field, with N at top of solenoid and S at bottom (or vice-versa).
Have you had the magnetic moment? The magnetic moment of the solenoid is a vector pointing axially, magnitude N I A,
N = no. of turns
I = current
A = cross-sectional area of solenoid.
It can be shown that the torque on any coil or bar magnet with mag moment μ is is τ = μ x B. (For a bar magnet the only way I know of determining μ is by measuring τ and B). So the torque on your solenoid about its y-axis is NIAB = πR² N I B which is just N times the torque developed in my post 18 for a single winding, as expected..

2. You can avoid the whole subject of the axial current by winding the solenoid as follows: Run one winding down the solenoid, top to bottom; then run a second winding back up but with the coil segments wound in opposite direction (cw, then ccw, for example) so that the axial currents cancel while the B field is doubled.