Four Wires and y component of magnetic field at center

[skibum143]

Homework Statement

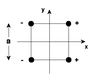
The four wires that lie at the corners of a square of side a=5.10cm are carrying equal currents i=2.40Amps into (+) or out of (-) the page, as shown in the picture.

Calculate the y component of the magnetic field at the center of the square.

Homework Equations

B field = u0 I / (2 pi r)
a^2 + b^2 = c^2

The Attempt at a Solution

Since at the origin there are two fields pointing up and to the right at 45 degrees, and two fields pointing up and to the left at 45 degrees, the total y component is 4 * sin45 * u0 I / (2 pi r).

r = sqrt [ (a/2)^2 + (a/2)^2 ] or 1.697

u0 = 4pi*10^-7

Using these numbers I got 8*10^-7 T but this is wrong. Can someone tell me what I'm doing wrong?

THanks!
Diagram is attached.

 

[collinsmark]

The Attempt at a Solution

Since at the origin there are two fields pointing up and to the right at 45 degrees, and two fields pointing up and to the left at 45 degrees, the total y component is 4 * sin45 * u0 I / (2 pi r).

So far, so good.

r = sqrt [ (a/2)^2 + (a/2)^2 ] or 1.697

Try plugging in the numbers again. The equation seems right, but not so much the 1.697 part.

 

[skibum143]

ah, stupid mistake. thanks for your help!