How to Determine the Correct Fourier Series for a Given Waveform?

[bizuputyi]

Homework Statement

Sketch the waveform and develop its Fourier series.

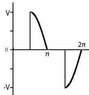
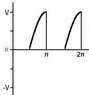
<br /> f(\omega t)=<br /> \begin{cases}<br /> 0 &amp; if &amp; 0 \leq \omega t \leq \frac{π}{2} \\<br /> V*sin(\omega t) &amp; if &amp; \frac{π}{2} \leq \omega t \leq π\\<br /> 0 &amp; if &amp; π \leq \omega t \leq \frac{3π}{2} \\<br /> V*sin(\omega t) &amp; if &amp; \frac{3π}{2} \leq \omega t \leq 2π<br /> \end{cases}<br />

Homework Equations

The Attempt at a Solution

I drew two sketches, please see attachment, I'm wondering which one is correct.

Calculating coefficients with V=1 just to see what the F.S. should look like, I've got:
a_0=0
a_n=\frac{1}{π}\left(\frac{2*sin\frac{nπ}{2}(-n+sin\frac{nπ}{2})}{-1+n^2} \right)
b_n=0

Now, if a0=0 that implies that the first sketch is correct. If bn=0 that means the function is even, well, none of my sketches is an even function, something is definitely wrong here. Also, I found even harmonics zero, so f(\omega t)=f(\omega t+π) which is true for the second sketch.

What did I do wrong? Thank you for looking into that.

 

[milesyoung]

If you just sketched \sin(x), where 0 \le x \le 2\pi, and superimposed it on your graphs, then which one is a match?

 

[bizuputyi]

The first one. That means bn can't be zero since this is not an even function, also it has half-wave symmetry, so f(\omega t)=-f(\omega t+π), my an calculation is wrong, so is bn.

 

[bizuputyi]

At least a0=0 for sure.

 

[milesyoung]

The first one ...

Right. But the periodic extension of that graph is neither an even or odd function.

 

[bizuputyi]

Exactly. The Fourier series must consist of both sine and cosine terms (i.e. an=something, bn=something), but with only odd harmonics.

 

[milesyoung]

Let me just go back to this:

If bn=0 that means the function is even ...

[STRIKE]It's true that an even function only has cosine terms in its Fourier expansion, but the converse statement isn't necessarily true, i.e. the Fourier expansion of a function can consist only of cosine terms without the function being even.[/STRIKE]

You just had an error in your Fourier coefficients. See below.

 

[olivermsun]

Let me just go back to this:

It's true that an even function only has cosine terms in its Fourier expansion, but the converse statement isn't necessarily true, i.e. the Fourier expansion of a function can consist only of cosine terms without the function being even.

Are you talking about functions which are even "almost everywhere"? I can't recall any "physical" functions which are odd but have only nonzero cosine terms, but I'd love to be reminded of an example.

 

[milesyoung]

[STRIKE]Your Fourier coefficients look correct btw. So good job :thumbs:[/STRIKE]

 

[milesyoung]

Are you talking about functions which are even "almost everywhere"? I can't recall any "physical" functions which are odd but have only nonzero cosine terms, but I'd love to be reminded of an example.

An odd function has only sine terms in its Fourier expansion, we can definitely agree on that

What I'm saying is that, if a function is odd, then that implies it only has sine terms in its Fourier expansion. That kind of statement is of the type:
<br /> p \Rightarrow q \qquad (1)<br />
If (1) is always true, then that doesn't necessarily mean that:
<br /> q \Rightarrow p<br />
is always true.

[STRIKE]The piecewise function included in the OP is an example of this.[/STRIKE]

 

[gneill]

Your Fourier coefficients look correct btw. So good job :thumbs:

Hmm. My own tinkering with the problem would indicate that there is a non-zero $b_0$, and the $a_n$ expression for n ≠ 0 looks suspicious to me. This is assuming that we're looking at the expressions in the first post.

Hint: You may need to use limits and L'Hopital to evaluate the coefficients when n = 1.

EDIT: That should be $b_1$ above, not $b_0$; Of course there's no 0-term for the b's.

 

[milesyoung]

Hmm. My own tinkering with the problem would indicate that there is a non-zero $b_0$, and the $a_n$ expression for n ≠ 0 looks suspicious to me. This is assuming that we're looking at the expressions in the first post.

Hint: You may need to use limits and L'Hopital to evaluate the coefficients when n = 1.

Doh, you're absolutely right. $b_1$ is non-zero. I can't find a problem with the expression for $a_n$ though or that $b_0 \neq 0$.

Edit: I'm not entirely sure why you're considering $b_0$.

 

[milesyoung]

Well, I've certainly put my foot in my mouth this time. I was racking my brain trying to find an example of how you could have only cosine terms in the Fourier series and for it not to be an even function.

Then I remembered that I'm an idiot and the sum of two even functions is even. Apologies to the OP and olivermsun.

 

[gneill]

Doh, you're absolutely right. $b_1$ is non-zero. I can't find a problem with the expression for $a_n$ though or that $b_0 \neq 0$.

Besides not matching what I derived myself, if I set the $a_n$ terms as given above and generate and plot f(x) it doesn't resemble the specified function at all. If I use my own derived terms I get a satisfying match to the function.

Edit: I'm not entirely sure why you're considering $b_0$.

That was just me typing faster than I was thinking

Of course there's no $b_0$. It's $b_1$ that's nonzero. I apologize for any confusion I may have stirred up.

 

[milesyoung]

Besides not matching what I derived myself, if I set the $a_n$ terms as given above and generate and plot f(x) it doesn't resemble the specified function at all. If I use my own derived terms I get a satisfying match to the function.

Hmm, I get the same values for $a_n$ as shown here:
http://www.wolframalpha.com/input/?i=Table%5Bint+1%2Fpi*Piecewise%5B%7B%7B0%2C0%3C%3Dx%3Cpi%2F2%7D%2C%7Bsin%28x%29%2Cpi%2F2%3C%3Dx%3Cpi%7D%2C%7B0%2Cpi%3C%3Dx%3C3*pi%2F2%7D%2C%7Bsin%28x%29%2C3*pi%2F2%3C%3Dx%3C2*pi%7D%7D%5D*cos%28n*x%29+from+x+%3D+0+to+2*pi%2C%7Bn%2C1%2C10%7D%5D

Which matches with those from the OP:
http://www.wolframalpha.com/input/?i=limit+1/pi*2*sin(n*pi/2)*(-n+sin(n*pi/2))/(-1+n^2)+as+n->1
http://www.wolframalpha.com/input/?i=Table[1/pi*2*sin(n*pi/2)*(-n+sin(n*pi/2))/(-1+n^2),{n,2,10}]

You get something different? I haven't tried plotting it.

 

[gneill]

Hmm, I get the same values for $a_n$ as shown here:
http://www.wolframalpha.com/input/?i=Table%5Bint+1%2Fpi*Piecewise%5B%7B%7B0%2C0%3C%3Dx%3Cpi%2F2%7D%2C%7Bsin%28x%29%2Cpi%2F2%3C%3Dx%3Cpi%7D%2C%7B0%2Cpi%3C%3Dx%3C3*pi%2F2%7D%2C%7Bsin%28x%29%2C3*pi%2F2%3C%3Dx%3C2*pi%7D%7D%5D*cos%28n*x%29+from+x+%3D+0+to+2*pi%2C%7Bn%2C1%2C10%7D%5D

Which matches with those from the OP:
http://www.wolframalpha.com/input/?i=limit+1/pi*2*sin(n*pi/2)*(-n+sin(n*pi/2))/(-1+n^2)+as+n->1
http://www.wolframalpha.com/input/?i=Table[1/pi*2*sin(n*pi/2)*(-n+sin(n*pi/2))/(-1+n^2),{n,2,10}]

You get something different? I haven't tried plotting it.

I retract my claim! While my expression for $a_n$ is different, they do yield the same values. No doubt we took a different trig-identity path somewhere along the line. I was fooled when the plotted results looked way off. However, when I plotted the OP's I failed to include the $b_1$ term! So yes, I goofed there.

 

[milesyoung]

I retract my claim! While my expression for $a_n$ is different, they do yield the same values. No doubt we took a different trig-identity path somewhere along the line. I was fooled when the plotted results looked way off. However, when I plotted the OP's I failed to include the $b_1$ term! So yes, I goofed there.

I tried plotting it and forgot to include the $a_1$ term. That was 30 min well spent staring at a graph. All's well that ends well!

 

[The Electrician]

Here's a plot:

 

[bizuputyi]

Thank you everyone for your comments.

It turns out my calculation was correct, however I keep getting b1=zero.

\frac{1}{π}\int_{\frac{π}{2}}^{π} sin(x)sin(nx)dx + \frac{1}{π}\int_{\frac{3π}{2}}^{2π} sin(x)sin(nx)dx = \frac{1}{π}\left( \frac{(-1+2cos(nπ)+2nsin(\frac{nπ}{2}))sin(nπ))}{-1+n^2}\right)

 

[milesyoung]

Are you using L'Hôpital's[/PLAIN] rule to determine the limit of that expression as $n \rightarrow 1$ or just plugging in $n = 1$ before you evaluate the integral? Both approaches should give $b_1 = \frac{1}{2}$:
http://www.wolframalpha.com/input/?...*pi}}]*sin(n*x)+from+x+=+0+to+2*pi)+for+n+=+1

 

[bizuputyi]

Unfortunately this is beyond my mathematics knowledge, I just plugged in n=1 for which denominator becomes zero.

 

[milesyoung]

... I just plugged in n=1 for which denominator becomes zero.

Ah, but the expression you arrive at for $b_n$ is undefined for $n = 1$ (division by zero is undefined). That denominator probably comes from the use of some trigonometric identity in evaluating the integral.

Try plugging in $n = 1$ before you evaluate the integral.

 

[bizuputyi]

Oh, I see, in that case I most certainly get b1=1/2. I'm sorry for my blindness, it's distance learning when I get stuck I'm on my very own.
I appreciate your help.

 

[milesyoung]

Nothing to be sorry about. Glad to be of help.

 

[Gremlin]

I have calculated a₀ = 0, which i found straight forward, and i have the calculation for a_n down the following:

a_n = 1/2π x[ [ ( (2 cos(nπ) ) / (1-n²) ) - ( (2 cos(n π/2) ) / (1-n²) )] + [ ( (2 cos(n 2π) ) / (1-n²) ) - ( (2 cos(n 3π/2) ) / (1-n²) )] ]

Does that look correct thus far can someone tell me?

 

[Gremlin]

I have calculated a₀ = 0, which i found straight forward, and i have the calculation for a_n down the following:

a_n = 1/2π x[ [ ( (2 cos(nπ) ) / (1-n²) ) - ( (2 cos(n π/2) ) / (1-n²) )] + [ ( (2 cos(n 2π) ) / (1-n²) ) - ( (2 cos(n 3π/2) ) / (1-n²) )] ]

Does that look correct thus far can someone tell me?

Anyone?

I'm struggling to collapse that any further. The opening poster obviously arrived at the correct answer so i can see what i am aiming for, am i on track to hit it?

 

[Gremlin]

cos α - cos ß = -2 sin ((α+ß)/2) sin ((α-ß)/2)

is what i need so for:

( (2 cos(nπ) ) / (1-n2) ) - ( (2 cos(n π/2) ) / (1-n2) )

I'd end up with

2/1-n² ((cos nπ) - cos(n π/2))

2/1-n² (-2 sin((nπ + n π/2) /2) x sin ((nπ - n π/2) /2) )

2/1-n² (-2 sin ((nπ + n π/2) /2) x ((nπ - n π/2) /2) )

I'm struggling at that point but i don't think I'm far away from the correct answer.

 

[Gremlin]

cos α - cos ß = -2 sin ((α+ß)/2) sin ((α-ß)/2)

is what i need so for:

( (2 cos(nπ) ) / (1-n2) ) - ( (2 cos(n π/2) ) / (1-n2) )

I'd end up with

2/1-n² ((cos nπ) - cos(n π/2))

2/1-n² (-2 sin((nπ + n π/2) /2) x sin ((nπ - n π/2) /2) )

2/1-n² (-2 sin ((nπ + n π/2) /2) x ((nπ - n π/2) /2) )

I'm struggling at that point but i don't think I'm far away from the correct answer.

Without the code, that's very hard to follow. My working is attached.

 

[gneill]

In post#15 milesyoung gave a link to a WolframAlpha calculation of a table of coefficients. Have you confirmed that your expression can match the given values? It would be unproductive to continue hammering away at trig identities if the initial expression is not correct.

 

[Gremlin]

I am trying to generate an expression for a_n - that's what I'm halfway through.

It looks to be in the right ballpark, but I've hit an impasse collapsing the expression. My working out is in post #28. I think i am losing the will to live!

 

[Gremlin]

Sorry i see what you're saying now. I shall try n=3 in what i have now and hope for 1/pi

 

[Gremlin]

No it doesnt.

 

[Gremlin]

I'm still trying, and failing, to nail this.

Can someone tell me where the attached goes off course please? There's not a lot to it, but already if n=3 i don't get 1/pi.

 

[gneill]

You're having problems with the integration. The arguments of the sine functions are not simple x's, so dx is not the differential element for them to be integrated as just a sine function. In other words,

$\int sin(u) du = -cos(u) + C$ which is fine since du is the differential element of u.

but if $u = (n+1) x$, then $du = (n + 1) dx$

You need to modify the integral so that the correct differential element is accounted for.

 

[Gremlin]

Ok thanks, i shall have another look.

 

[Birchyuk]

Good evening,

I am also struggling on this question and have been for a solid week.

I am currently trying to calculate a_n. I so far have:

I have assumed for the time being x=wt

\int sinxcosnx.dx
\frac{1}{2} \int sin(n+1)x+sin(n-1)x.dx
\frac {1}{2} (\frac {-cos(n+1)x} {n+1} + (\frac {-cos(n-1)x}{n-1})

I have input the limits of x between pi and \frac {pi}{2} and subtracted there. Furthermore i have done the same to 2pi and \frac {3pi}{2} and added these but my result continually comes out at 0. I am expecting only odd numbers of n will produce a result. I have tried a few methods but none of them seem to be working.My hunch is that I am not integrating correctly or I am misunderstanding the relevance of (wt)?

Any assistance would be appreciate greatly.

 

[bizuputyi]

Hi Birchyuk,

Try this:

a_n = \frac{1}{\pi} \int sinxcosx.dx + \frac{1}{\pi} \int sinxcosx.dx

Insert your limits and put the equation in wolfram or mathlab. What do you get?

'V' won't make any difference as long as it's 1 but to be accurate 'V' should also be in the equation.

 

[Birchyuk]

Hi bizuputyi,

Thanks for the reply

Inputting this i get the following:

https://www4c.wolframalpha.com/Calculate/MSP/MSP103820ai5432f8fdg93e0000303fdbg66ci2bbf8?MSPStoreType=image/gif&s=4 and https://www5b.wolframalpha.com/Calculate/MSP/MSP8661cb3a0cb5a74g28300003gh8hbag7c679080?MSPStoreType=image/gif&s=33

I have produced a table in wolfram which is as below: (i have to admit i am not an expert with wolfram)

http://www.wolframalpha.com/input/?...n*3*pi/2))+(cos(n*2*pi))))/(n^2-1)),{n,2,10}]

This again shows i have both even and odd harmonics which i believe is wrong

 

[bizuputyi]

I know this is a shortcut but it is perfectly acceptable to produce this:

http://www.wolframalpha.com/input/?...2*pi}}]*cos(n*x)+from+x+=+0+to+2*pi,{n,1,10}]

Then put a1, a3, a5... in your F.S final result.

 

[Birchyuk]

Hi Bizuputyi,

Thanks for this. For my own piece of mind what is going wrong as this does not make sense to me why this is not working the way i think it should?

Thanks.

 

[macca67]

Hi Guys,

I am really struggling with this same question, here is what I have done so far, but there is a mistake (a few probably) in there and I can't find it!

fx=Vsin (wt)
x=wt

So a₀= 1/π∫f(x)dx

= V/π∫sin (x) dx [lim π/2 to π] + V/π∫sin (x) dx [lim 3π/2 to 2π]

So next I integrated the above to give
=V/π[-cosx] [lim π/2 to π] + V/π[-cosx] [lim 3π/2 to 2π]
=V/π[0]
=0

so I proved a₀=0

Next on to a_n

a_n= V/π∫sin (x).cos (nx) dx [lim π/2 to π] + V/π∫sin (x).cos (nx) dx [lim 3π/2 to 2π]

using the trig rule 2sin A.cos B = [sin (A+B) + sin (A-B)]/2 I changed the above to

a_n= V/2π∫sin (x+nx)+sin (x-nx) dx [lim π/2 to π] + V/2π∫sin (x+nx)+sin (x-nx) dx [lim 3π/2 to 2π]

this was then integrated to give

= V/2π[(-cos(x+nx)/n+1)-(cos(x-nx)/n-1)]+V/2π[(-cos(x+nx)/n+1)-(cos(x-nx)/n-1)]

When I put n=1 it all cancels out to 0, but by what's written in this thread I should have -2(V/2π) to give (-V/π)

For b_n I end up with

b_n=V/2π∫cos (x-nx)-cos (x+nx) dx [lim π/2 to π] + V/2π∫cos (x-nx)-cos (x+nx) dx [lim 3π/2 to 2π]

which integrated to

V/2π[(sin(x).cos(x)-(x-sin (x))] [lim π/2 to π] +V/2π[(x-1/4sin(4x))-(x-sin1/3(3x))] [lim 3π/2 to 2π]

b_n=1/2 when n=1 (I put the n=1 in before integration as suggested by Gneil to get this, I don't understand why it should make a difference though?)

where have I gone wrong?

I think b_n is correct, but my a_n isn't

any help gratefully received!

EDIT- Just noticed the red bit above is wrong, not doing too well here!

 

[macca67]

One theory I have is when I use the trig rule, I change the sin(x) of the b_n function to a cos then when I integrate it goes back to a sin, after integration should b_n= (something) cos(something)?

 

[macca67]

ok,

b_n now sorted using integration by parts.

Still having difficulty with a_n