kickstar
- 7
- 0
I'm asked to transform y(t) = x(t)*x(t) (where * is the convolution product) and x(t)= sinc(t)cos(2π10t) ( sinc(t)= sin(πt)/(πt) ).The attempt at a solution
Clearly everything is simple if you know X(f), because y(t)=InverseFourier{ X(f)2 }. The problem is that I can't find X(f). By the way, because x(t) is even, I can use the easier version of the transform, but it doesn't help so much, in the end I have to solve:
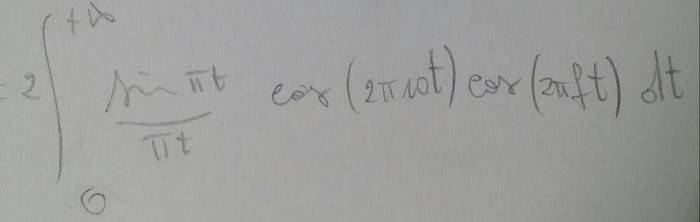
I tried in vain with some trigonometric formula, but I still have product of sin/cos in the end.
Trying with the convolution product doesn't help either, because I get this:
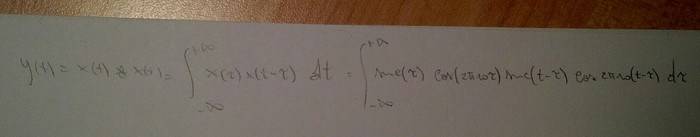
And I can't see anything that may help me...Wolfram says this is the solution:
EDIT: wait a minute! I'm dumb! because I can use the modulation theorem...
Clearly everything is simple if you know X(f), because y(t)=InverseFourier{ X(f)2 }. The problem is that I can't find X(f). By the way, because x(t) is even, I can use the easier version of the transform, but it doesn't help so much, in the end I have to solve:
I tried in vain with some trigonometric formula, but I still have product of sin/cos in the end.
Trying with the convolution product doesn't help either, because I get this:
And I can't see anything that may help me...Wolfram says this is the solution:
1/4 sqrt(pi/2) (sgn(-w-20pi+1)+sgn(-w+20pi+1)+sgn(w-20pi+1)+sgn(w+20pi+1))
EDIT: wait a minute! I'm dumb! because I can use the modulation theorem...