Free body diagram of man in a box

Click For Summary
SUMMARY

The discussion revolves around a physics problem involving a 60 kg man standing in a 30 kg box on a weighing machine. The key question is determining the weight displayed by the machine when the box is at rest due to the man's force applied via a rope. The correct answer is 15 kg, as indicated in the textbook, which suggests that the net force acting on the system must be analyzed using free body diagrams for both the man and the combined man-box system.

PREREQUISITES
  • Understanding of Newton's laws of motion
  • Knowledge of free body diagrams
  • Basic concepts of forces and weight
  • Ability to analyze static equilibrium
NEXT STEPS
  • Study free body diagram techniques in physics
  • Learn about static equilibrium and its applications
  • Explore Newton's laws of motion in detail
  • Practice problems involving forces and weight calculations
USEFUL FOR

Students studying physics, particularly those focusing on mechanics and force analysis, as well as educators looking for examples of free body diagrams in problem-solving scenarios.

1/2"
Messages
98
Reaction score
0

Homework Statement


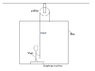
A 60 kg man stands in a 30 kg box on a light weighing machine.
If the box is kept at rest due to force applied by the man by the rope , what is the weight shown by the weighing machine?


Homework Equations





The Attempt at a Solution


.answer given in book is 15 kg.
But if the net force man i think will his weight-weight of the box=300N
I don't think i am proceeding correctly.
I just need a hint for the free body diagram.
Thanks in advance
 

Attachments

  • Untitled.png
    Untitled.png
    2 KB · Views: 499
Physics news on Phys.org
hi 1/2"! :wink:

as often in these problems, you need two free body diagrams …

in this case, one for the man (on his own), and one for the man-and-box …

how many external forces forces are there in each case? :smile:​
 

Similar threads

Potential Mistake in Free-Body Diagram
  • · Replies 5 ·
Replies
5
Views
2K
Is it friction or tension acting on the person hanging on a rope?
  • · Replies 4 ·
Replies
4
Views
1K
Rocket + Connected Body Dynamics problem
  • · Replies 47 ·
2
Replies
47
Views
3K
Free Body Diagram of Mass-Spring System
  • · Replies 5 ·
Replies
5
Views
2K
Calculating Distance: Free Body Diagram for Box Sliding with Friction
  • · Replies 1 ·
Replies
1
Views
2K
Block on top of an inclined plane, with a rough surface, that moves with constant acceleration
  • · Replies 41 ·
2
Replies
41
Views
4K
Finding Radial Force from Free Body Diagram
  • · Replies 4 ·
Replies
4
Views
2K
Free body Diagram of a Plank resting on two Cylinders
  • · Replies 14 ·
Replies
14
Views
3K
What Forces Are Acting on a Man Climbing an Incline?
  • · Replies 8 ·
Replies
8
Views
18K
Solving Free-Body Diagrams for Moving Nuts on Rods: Tips and Techniques
  • · Replies 9 ·
Replies
9
Views
2K