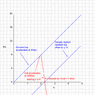
Yes, for as long as the bolt was part of the elevator, it was being accelerated by the same force that was accelerating the rest of the elevator.
When something is dropped, it just means that it is no longer traveling as part of whatever platform it was dropped off of.
The bolt, still connected to the elevator, was accelerated for some time to the velocity of the elevator. 8 \tfrac{m}{s}
At that point, it broke off. What force, exactly, changed its velocity from 8 \tfrac{m}{s} to 0 \tfrac{m}{s}?
That's right, none.
And according to Newton's First Law:
An object in motion tends to stay in motion, and an object at rest tends to stay at rest unless acted upon by an external force.
With no force to "remove" its initial velocity (Since it was traveling along with the elevator), the velocity of the bolt remains the same as it was the instant it detached from the elevator.
Just like how an object you drop out of the window of a moving car, has an initial velocity that's the same as that of the car the moment it was dropped.