- #1
JasMath33
- 21
- 1
I have been interested in this idea of the FDQR. This idea states the following.
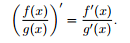
I have been trying to see if there is some 2 functions which make this true, but have not found it on research or with trying functions. Does anyone have any insight on this. I think it is just neat and want to know more about what people know about it.
I have been trying to see if there is some 2 functions which make this true, but have not found it on research or with trying functions. Does anyone have any insight on this. I think it is just neat and want to know more about what people know about it.