Friction between boxes - please check if this is right

[iJamJL]

Homework Statement

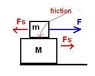
Small block 1 with mass m = 2.19 kg sits on top of large block 2 of mass M = 7.0 kg, and the pair sit on a frictionless, horizontal table. Between the blocks: the coefficient of kinetic friction is μk = 0.247, and the coefficient of static friction is μs = 0.319. Find the magnitude of the maximum force applied horizontally to the upper block (block 1) that will cause the two blocks to slide together.

Homework Equations

Frictional force = μ*Normal
F=ma

The Attempt at a Solution

If we want to keep the two blocks together, then we need to use static friction. The frictional force should equal the force that is pushing the upper box so that it doesn't slip off the bottom box.

Therefore:

Ff = μs * N
= .319 * 2.19 * 9.81 = 6.85

This is obviously wrong, but that is what I began with originally. The only other idea that comes to mind is if we add the sums of the masses instead of only the top box.

Ff = μs * N
= .319 * (2.19+7.0) * 9.81 = 28.76

I don't know which is correct, or if both are wrong.

 

[ehild]

The force has to accelerate both blocks, as if they were stuck together.

ehild

 

[iJamJL]

The force has to accelerate both blocks, as if they were stuck together.

ehild

Well, in that case, then the second solution would be correct. However, the answer is not 28.76. I'm stuck at this point.

 

[ehild]

It does not mean that your solution is correct. Remember, there is no friction between the floor and the big block. The force you wrote up is the maximum force applied to a block 9.19 kg so as it do not start moving. The question is with what force at maximum you can pull the upper block so both blocks accelerate together. Write the FBD and equation of motion for both blocks. Find the common acceleration. From the acceleration, find the force of static friction. What is its maximum value?

ehild

 

[iJamJL]

It does not mean that your solution is correct. Remember, there is no friction between the floor and the big block. The force you wrote up is the maximum force applied to a block 9.19 kg so as it do not start moving. The question is with what force at maximum you can pull the upper block so both blocks accelerate together. Write the FBD and equation of motion for both blocks. Find the common acceleration. From the acceleration, find the force of static friction. What is its maximum value?

ehild

ehild:

Thanks for your replies.

I do have to admit that this is hardest part for me (and I assume for everyone else). I have trouble setting this up properly.

If the two blocks were to be thought of as one big block, then the frictional force is the amount that we can push the upper block so both move together in unison. To find acceleration:

Ff = ma
28.76 = 9.19*a
a=3.12939

Then to find the force to push the top block:
F = m(top)*a
F = 2.19*3.12939
F = 6.853

What do we do from there? Or where did I make a mistake?

 

[iJamJL]

lol I haven't gotten past that part yet..

Could you offer a different way of looking at it?

 

[ehild]

The friction is an internal force for the system of two blocks. If the upper block moves to the right, the static friction Fs acts to the left,

F-Fs=m a₁

and it is only the friction pointing to the right that accelerates block 2.

Fs=M a₂

The blocks move together, so a₁=a₂=a Add up the equations: The internal force Fs cancels:

F-Fs+Fs=ma+Ma

F=(m+M)a

The blocks move together as a single body with mass m+M, under the effect of the external force F.

Fs can not exceed μmg. What is the maximum acceleration of M? What does it mean for F?


ehild

 

[iJamJL]

I'm still struggling.

I understand how you got to F=(m+M)a and that the blocks move together.

You said that Fs can not exceed μmg:

Fs=(.319)(9.19)(9.81)=28.759
μmg=(.319)(2.19)(9.81)=6.853

So that means that F+μmg=Fs
F=Fs-μmg
F=21.906

The acceleration of block M would be:

Ff=μMg
=.319*7*9.81
=21.906

21.906=ma
21.906/7.0=3.12939I'm still looking at this incorrectly..

I'm sorry. This must be frustrating.
The other way that I thought of solving this is:

F+μmg=Fs
F=Fs-μmg
(M+m)*a=21.906
a=2.38

We take this and apply it to the upper block:

F=ma
F=2.19*2.38
F=5.21

 

[ehild]

=iJamJL;3787064
You said that Fs can not exceed μmg:

Fs=(.319)(9.19)(9.81)=28.759

NO.

I mean that Fs is the force of static friction that acts between the blocks. The small block (of mass m) presses the bigger one, there is F_N=mg normal force between them and the maximum static friction is this normal force multiplied by μ.

Fs≤μmg=(.319)(2.19)(9.81)=6.853 N. You can take Fs=6.853 N.

The force of friction accelerates the bigger block: a=Fs/M. Calculate a.

The applied force accelerates both blocks:

F=(m+M)a. Calculate F.

ehild