Friction Coefficient for Brake Pads: Validity of F=2x(UN) Equation?

AI Thread Summary
The discussion revolves around determining the friction coefficient of brake pads using the equation F=2x(UN) versus F=UxN. The user is conducting tests where a brake disc is pulled between two pads, measuring the force required for slippage. They question the validity of using F=2x(UN) under the assumption that both pads exert identical forces and coefficients of friction. The conversation highlights that both equations are referenced in various contexts, suggesting that the choice depends on the specific testing scenario. Ultimately, clarity on the application of these equations is essential for accurate friction coefficient determination.
protector
Messages
3
Reaction score
0
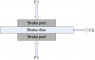
I've been trying to figure out the friction coefficient of some brake pads. My test fixture only allows me to pull (F2) a brake disc between two brake pads clamped around the disc with a force F1. I then measure with a load cell the maximum force required for the brake disc to slip.

My question is simply, will the basic equation F=UxN be valid, or is it correct to assume that F= 2x(UN) in this scenario assuming F1 and U is identical for both brake pads?

I've been googling the topic and my impression is that both equations are used.
 

Attachments

  • friction.PNG
    friction.PNG
    4.2 KB · Views: 615
Physics news on Phys.org
Should be F=2 x (UN). Imagine replacing one of the pads with a frictionless pad and then you'd get F = 1 x (UN) for the one pad with friction.
 

Thread 'Derivation of Hamilton's Principle: Questions'

I have recently been really interested in the derivation of Hamiltons Principle. On my research I found that with the term ##m \cdot \frac{d}{dt} (\frac{dr}{dt} \cdot \delta r) = 0## (1) one may derivate ##\delta \int (T - V) dt = 0## (2). The derivation itself I understood quiet good, but what I don't understand is where the equation (1) came from, because in my research it was just given and not derived from anywhere. Does anybody know where (1) comes from or why from it the...
View full post »

Similar threads

Braking force required on the disc brake pads
Replies
14
Views
9K
Automotive How to calculate hydraulic disc brake size using actuation force?
Replies
15
Views
6K
Problem in getting correct coefficients of frictional forces
Replies
9
Views
1K
Centripetal force and spinning discs
Replies
17
Views
5K
Is a heat vs Mu chart Misleading? What factors into Mu? (brake pads)
Replies
2
Views
7K
Find torque in disc brakes given normal force and coefficient of friction
Replies
1
Views
9K
Capstan Equation, Friction and Normal Force
Replies
14
Views
2K
Friction in a brakepad/brakedisc scenario,
Replies
11
Views
8K
Dependence of friction on area.
Replies
6
Views
2K
Frictional toruq of a brake disc
Replies
3
Views
3K

Hot Threads

Recent Insights

Back
Top