Fridge on truckutter frustration

[Rockdog]

I've included a pic.

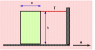
A refrigerator is approximately a uniform parallelepiped h = 8 ft tall, w = 3 ft wide, and d = 2 ft deep. It sits upright on a truck with its 3 ft dimension in the direction of travel. Assume that the refrigerator cannot slide on the truck and that its mass is 110 kg. For the first three parts of this problem, the rope shown in the picture is not there.

a) When the truck is not accelerating, what is the normal force exerted on the refrigerator by the truck bed?
b) If the truck now accelerates at 2 m/s2, what is the horizontal force exerted on the refrigerator by the truck bed?
c) What is the maximum acceleration the truck can have such that the refrigerator does not tip over?
==========================
d) Suppose now that a rope connects the top of the refrigerator with the cab of the truck, which now accelerates at twice the acceleration calculated in (c). The refrigerator lifts off slightly at the front but is held in place by the horizontal rope. Find the tension in the rope.

Ok. Part a and b were trivial.

I'm stuck badly on part c and d. I know I got to do a net torque equation here, but not sure how to write it up.

The hints for part c weren't that much help.
It says "Since the fridge is not rotating, the sum of all the torques about an axis through the CM must be zero.
and For the maximum acceleration, assume that the fridge is just starting to tip, so that the point of contact with the floor of the truck is at the back corner.

So yea, still stuck.

part d)
Similiar to part c. Not sure how to go about writing the equations. :(

 

[NateTG]

So in the reference frame of the refrigerator you've got the following forces:
the normal force
the force of gravity
friction between the truck and the refrigerator
the 'inertial force' which represents the fact that the refrigerator is in an accelerated reference frame.

the acceleation force and gravity exert zero net torque about the CM.

The FBD redily gives that the normal force is equal to mg and the force of friction is equal to ma.

As the refrigerator tips over the back edge, the normal force exerts torque about the CM since it's only applying at the back edge of the refrigerator. Similarly, friction is only applying at the back edge of the refrigerator. You know that the net torque zero, what more do you need?

 

[M98Ranger]

I completely understand your frustration with this problem. It can be difficult to visualize and apply the correct equations in these types of situations. Let's break down the problem step by step and see if we can find a solution together.

a) When the truck is not accelerating, the normal force exerted on the refrigerator by the truck bed is simply equal to the weight of the refrigerator, which is given by Fg = mg = (110 kg)(9.8 m/s^2) = 1078 N. This is because the refrigerator is at rest and there are no other forces acting on it.

b) Now, when the truck accelerates at 2 m/s^2, there will be a horizontal force acting on the refrigerator, which we can calculate using Newton's second law, F = ma. This force will be in the direction opposite of the acceleration, so it will be equal to F = (110 kg)(2 m/s^2) = 220 N.

c) To find the maximum acceleration the truck can have without tipping the refrigerator, we need to consider the torque being exerted on the refrigerator. As the hint suggests, we can use the fact that the sum of all torques must be zero to find the maximum acceleration.

Let's assume that the point of contact between the refrigerator and the truck bed is at the back corner, as suggested in the hint. This means that the distance from the point of contact to the center of mass (CM) of the refrigerator is d = √(h^2 + w^2)/2 = √(8^2 + 3^2)/2 = 4.47 ft.

Now, the torque being exerted on the refrigerator by the force of gravity is given by τ = Fd = (1078 N)(4.47 ft) = 4823.66 N·ft. This torque is trying to tip the refrigerator over in a clockwise direction.

To counteract this torque, there must be an equal and opposite torque acting in the counterclockwise direction. This torque is caused by the horizontal force exerted on the refrigerator by the truck bed. We can calculate this torque using τ = Fr, where r is the distance from the point of contact to the point where the force is being applied. In this case, r = w/2 = 1.5 ft.

Setting these two torques equal to each other, we get Fr = Fd, or