What is the equation of the extreme normal line for a parabola?

[MarkFL]

View attachment 1225

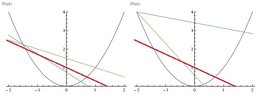
The curve in the figures above is the parabola $y=x^2$. Let us define a normal line as a line whose first quadrant intersection with the parabola is perpendicular to the parabola. Five normal lines are shown in the figures above.

For a while, the $x$-coordinate of the second quadrant intersection of a normal line with the parabola gets smaller as the $x$-coordinate of the first quadrant intersection gets smaller. But eventually a normal line's second quadrant intersection gets as small as it can get.

The extreme normal line is shown as a thick red line in the figures above. Once the normal lines pass the extreme normal line, the $x$-coordinate of the second quadrant intersections with the parabola start to increase.

The figures above show two pairs of normal lines. The two normal lines of a pair have the same second quadrant intersection with the parabola, but one is above the extreme normal line (in the first quadrant) and the other is below it.

(a) Find the normal line pair associated with a particular second quadrant intersection with the parabola.

(b) Hence, or otherwise, find the equation of the extreme normal line.

(c) Find the normal line that traps the smallest area between it and the parabola.​

 

[anemone]

My solution:

Spoiler

Part (a):

If we let the point $(k, k^2)$ where $k>0$ be any point that lies on the parabola $y=x^2$ in the first quadrant, then the gradient of the tangent line is $\frac{dy}{dx}=2x=2k$ and the gradient of the normal line is the negative reciprocal of the gradient of the tangent line, i.e. $-\frac{1}{2k}$.

Thus, the equation of the normal line that passes through $(k, k^2)$ with gradient $-\frac{1}{2k}$ is

\(\displaystyle y-k^2=-\frac{1}{2k}\left(x-k\right)\)

\(\displaystyle 2ky-2k^3=-(x-k)\)

\(\displaystyle 2ky+x=2k^3+k\)

and the intersection point of this normal line with the curve of the parabola on the second quadrant can be found by solving the equations $2ky+x=2k^3+k$ and $y=x^2$ simultaneously and we get \(\displaystyle \left(-\frac{1+2k^2}{2k},\frac{(1+2k^2)^2}{4k^2}\right)\) as the intersection point of the normal line and the parabola on the second quadrant.

Part (b):

If we relate \(\displaystyle x=-\frac{1+2k^2}{2k}\), we can find the maximum $x$ (the x-coordinate intersection point between the extreme normal line and the curve) by using the calculus method.

\(\displaystyle x=-\frac{1+2k^2}{2k}\)

\(\displaystyle \frac{dx}{dk}=-\frac{(-4k)(2k)-(-(1+2k^2))(2)}{4k^2}=\frac{1-2k^2}{2k^2}\) and \(\displaystyle \frac{d^2y}{dx^2}=-\frac{1}{k^2}\). (This implies no matter what the $k$ value that we get, it must yield a maximum $x$.)

We see that \(\displaystyle \frac{dy}{dx}=0\) iff \(\displaystyle k=\pm\frac{1}{\sqrt{2}}\) and bear in mind that in our case, $k>0$ so the maximum $x$ occurs at \(\displaystyle k=\frac{1}{\sqrt{2}}\)

and therefore, the equation of the extreme normal line is

\(\displaystyle 2(\frac{1}{\sqrt{2}})y+x=2(\frac{1}{\sqrt{2}})^3+(\frac{1}{\sqrt{2}})\)\(\displaystyle \sqrt{2}y+x=\sqrt{2}\)

Part (c):

We want to minimize the area (A) between the normal line and the parabola and again, we will tackle this last part of the problem using calculus method.

View attachment 1231

\(\displaystyle A=\int_{-\frac{1+2k^2}{2k}}^k \left(\frac{2k^3+k-x}{2k}-x^2\right)=\frac{4k^3}{3}+\frac{1}{48k^3}+k+\frac{1}{4k} \)

\(\displaystyle \frac{dA}{dk}=\frac{64k^6+16k^4-4k^2-1}{16k^4}=\frac{(4k^2+1)(16k^4-1)}{16k^4}\)

and \(\displaystyle \frac{d^2A}{dk^2}=8k+\frac{1}{4k^5}+{1}{2k^3}>0\) since $k>0$.

Therefore, A is at its minimum when $16k^4-1=0$ or \(\displaystyle k=\frac{1}{2}\).

At \(\displaystyle k=\frac{1}{2}\), the normal line's equation is

\(\displaystyle 2(\frac{1}{2})y+x=2(\frac{1}{2})^3+\frac{1}{2}\)
\(\displaystyle

y+x=\frac{3}{4}\)

 

[MarkFL]

I just spent several hours typing up my solution, only to have my power go out for a moment as I was nearing completion and everything I worked on was lost. I may or may not do it all over again. (Angry)

 

[anemone]

I just spent several hours typing up my solution, only to have my power go out for a moment as I was nearing completion and everything I worked on was lost. I may or may not do it all over again. (Angry)

Hey MarkFL, I'm so sorry that this happened...and let's just "ignore" this problem for now...(Nerd)

 

[MarkFL]

Thank you for your solution anemone! I can only give you partial credit for part (a) as I asked for the pair of normal lines associated with a particular second quadrant solution, but I applaud your tackling of such a difficult problem! (Clapping)

Here is my solution:

Spoiler

I wanted to generalize a bit and let the curve be $f(x)=ax^2$, where $0<a$. Let the first quadrant intersection between a normal line and the parabola be $\left(p,ap^2 \right)$ and the second quadrant intersection be $\left(q,aq^2 \right)$.

Because the normal line as defined is perpendicular to the parabola at the first quadrant intersection, we may express the slope $m$ of the normal line as:

\(\displaystyle m=-\frac{1}{f'(p)}=-\frac{1}{2ap}\)

Using this slope, the first quadrant point of intersection, and the point-slope formula, we find then that the normal line is given by:

\(\displaystyle y-ap^2=-\frac{1}{2ap}(x-p)\)

Arranging this in slope-intercept form, we obtain the general normal line:

(1) \(\displaystyle y=-\frac{1}{2ap}x+\frac{2a^2p^2+1}{2a}\)

(a) To find the pair of normal lines associated with a particular second quadrant intersection, we may equate two expressions for the slope of the normal line:

\(\displaystyle m=\frac{aq^2-ap^2}{q-p}=-\frac{1}{2ap}\)

\(\displaystyle a(q+p)=-\frac{1}{2ap}\)

Writing this equation in standard quadratic form in $p$, there results:

\(\displaystyle p^2+qp+\frac{1}{2a^2}=0\)

Application of the quadratic formula yields:

\(\displaystyle p=\frac{-aq\pm\sqrt{a^2q^2-2}}{2a}\)

Using these values for $p$, we obtain the pair of normal lines:

\(\displaystyle y=-\frac{1}{2a\left(\frac{-aq\pm\sqrt{a^2q^2-2}}{2a} \right)}x+\frac{2a^2\left(\frac{-aq\pm\sqrt{a^2q^2-2}}{2a}

\right)^2+1}{2a}\)

Simplifying, we obtain:

\(\displaystyle y=\frac{1}{aq\pm\sqrt{a^2q^2-2}}x+\frac{q\left(aq\pm\sqrt{a^2q^2-2} \right)}{2a}\)

Thus, for the posted problem, where $a=1$, we have the pair of normal lines:

\(\displaystyle y=\frac{1}{q\pm\sqrt{q^2-2}}x+\frac{q\left(q\pm\sqrt{q^2-2} \right)}{2}\)

(b) To find the extreme normal line, we need only equate the discriminant to zero in the solution for $p$ for a given normal line pair, that is to take the pair which are the same line:

\(\displaystyle p=-\frac{q}{2}\)

Now, using the equation:

\(\displaystyle p^2+qp+\frac{1}{2a^2}=0\)

and solving for $q$, we get:

\(\displaystyle q=-\frac{2a^2p^2+1}{2a^2p}\)

Hence:

\(\displaystyle p=\frac{2a^2p^2+1}{4a^2p}\)

Solving this for $p$, we find:

\(\displaystyle p=\frac{1}{a\sqrt{2}}\)

Substituting this value of $p$ into (1), we obtain the extreme normal line:

\(\displaystyle y=-\frac{1}{\sqrt{2}}x+\frac{1}{a}\)

For the posted problem, the extreme normal line is:

\(\displaystyle y=-\frac{1}{\sqrt{2}}x+1\)

We may also use the calculus to determine the extreme normal line by minimizing $q$. Recall we found:

\(\displaystyle p^2+qp+\frac{1}{2a^2}=0\)

Implicitly differentiating with respect to $p$, we find:

\(\displaystyle 2p+q+p\frac{dq}{dp}=0\)

\(\displaystyle \frac{dq}{dp}=-2-\frac{q}{p}\)

Equating this to zero, we find:

\(\displaystyle p=-\frac{q}{2}\)

Finding the extreme normal line now follows the same method as above.

(c) To find the normal line that traps the minimal area $A$ between it and the parabola, we may begin by expressing this area as:

\(\displaystyle A=\int_q^p -\frac{1}{2ap}x+\frac{2a^2p^2+1}{2a}-ax^2\,dx\)

The number and nature of the extrema will not depend upon the value of $a$, so first let's let $a=1$:

\(\displaystyle A=\int_{-\left(p+\frac{1}{2p} \right)}^p -\frac{1}{2p}x+ \frac{2p^2+1}{2}-x^2\,dx\)

Completing the square on the integrand, we have:

\(\displaystyle A=\int_{-\left(p+\frac{1}{2p} \right)}^p \left(p+\frac{1}{4p} \right)^2-\left(x+\frac{1}{4p} \right)^2\,dx\)

Using the substitution:

\(\displaystyle u=x+\frac{1}{4p}\,\therefore\,du=dx\)

and the even function rule, we may write:

\(\displaystyle A=2\int_{0}^{p+\frac{1}{4p}} \left(p+\frac{1}{4p} \right)^2-u^2\,du\)

Applying the FTOC, we find:

\(\displaystyle A=\frac{4}{3}\left(p+\frac{1}{4p} \right)^3\)

Differentiating with respect to $p$, we find:

\(\displaystyle \frac{dA}{dp}=4\left(p+\frac{1}{4p} \right)^2\left(1-\frac{1}{4p^2} \right)\)

Equating this to zero, we find the only real root comes from:

\(\displaystyle 4p^2-1=(2p+1)(2p-1)=0\)

Taking the positive root, our one critical value is:

\(\displaystyle p=\frac{1}{2}\)

The first derivative test easily confirms that this a minimum.

And so, using (1), the normal line that traps the minimal area is:

\(\displaystyle y=-x+\frac{3}{4}\)

Using the same reasoning, the normal line trapping the minimal area for an arbitrary $a$ is when:

\(\displaystyle p=\frac{1}{2a}\)

Using (1) again, the normal line that traps the minimal area is:

\(\displaystyle y=-x+\frac{3}{4a}\)

And so we find the minimal trapped area to be:

\(\displaystyle A_{\min}=\frac{4}{3a^2}\)