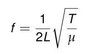Fundamental Frequency of a nano scale oscillator (graphene)

[maguirpi]

Hi everyone, long time lurker, first time poster.

I've just begun a phd which involves nanoribbons (a small strip of a 2D material connected at either end to a larger 'bulk' section of the same 2D material). A question has occurred to me. These nanoribbons look a lot like a piece of string in a violin/sonometer (although the tension is obviously not easily tuneable). This means that they should have a frequency of vibration like a piece of string in classical experiments. I'd really like to estimatethis (for fun, not homework or anything like that).

Using electron and ion microscopy we know what the width, height and breadth are. We know the density as we know the material. So basically in the equation attached, what we don't know is the tension. I guess this is going to be quite small anyway. The only thing I can think to do is estimate the number of atoms at each end and use the bond energy/distance. This will allow me to calculate a total force and use this as my upper bound on tension. I'm totally open to other ideas though, maybe using material properties or a different approach. My classical mechanics might be rusty too!

If you need anything clarified as well please just ask.

Thanks in advance for your help,
Maguirpi

 

[Baluncore]

The vibration of a string is based on the assumption that the tension is independent of the displacement and that the restoring force is determined by displacement. Frequency is then not dependent on amplitude.

With a ribbon having zero tension at the zero displacement, the frequency of oscillation will be amplitude dependent. It will flap like a flag in the wind.

 

[AlephZero]

I suspect your "ribbon" is better described as a beam fixed at both ends. If you know Young's Modulus (or since grapheme is unlikely to be an isotropic material, the relevant modulus along the length of the ribbon) you can estimate the lowest natural frequency here: http://faculty.uml.edu/pavitabile/22.403/web_downloads/Frequencies_of_Common_Systems.PDF

If there is any axial tension the frequency will increase. See here:
http://www.vibrationdata.com/tutorials2/beam_axial_load.pdf

Since a beam has some elastic stiffness when the tension is zero, unlike a string, the effect of amplitude on frequency will to be second-order, so you can ignore it for reasonably small vibration amplitudes (i.e. when amplitude is the same order of magnitude as the thickness of the ribbon)

 

[Baluncore]

This certainly is an interesting question.

Maybe it comes down to the thickness of the ribbon. Being described as 2D suggests a zero thickness which makes it more like a catenary chain than a beam.

There will be a mode where the ribbon oscillates sideways within its 2D plane. That will certainly conform to the beam model and have a higher frequency than waves propagating along the same catenary chain. The frequency will be independent of the ribbon thickness.

 

[Baluncore]

Probably the closest mechanical model of a 2D graphene ribbon would be a static, multi-strand, roller chain.
http://www.meritchain.com/products/ss-chains/Multi-Strand-Roller-Chain.jpg