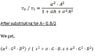- #1
issac newton
- 14
- 0
i have attached a bode plot and the opamp dc second order lpf circuit. the opamp Tl082 has a gain bandwidth product of 4Mhz according to the datasheet. this circuit has a bandwidth of 414.25khz. can we determine the opamp' individual gain-bandwidth product from this plot ??
if yes , how do we find the answer ?
if yes , how do we find the answer ?