- #1
PhyAmateur
- 105
- 2
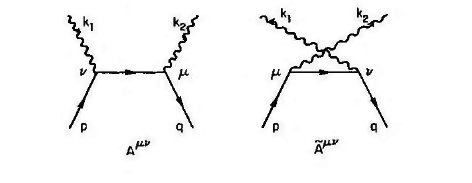
My book says that in this case $$e^+e^- \rightarrow \gamma \gamma $$ gauge invariance requires that $$k_{1\nu}(A^{\mu\nu} + \tilde{A}^{\mu\nu})=0=k_{2\mu}(A^{\mu\nu} + \tilde{A}^{\mu\nu})$$ Please see attachment. My question is how does this statement hold?

Last edited: