Emilijo
- 35
- 0
Homework Statement
I need to get a general function in 2 variables f(m,n).
The task is to find a general function f(m,n) with these terms:
The function has to be periodic.
The function has to include those blue and red points in each example.
The value of the function has to be f(m,n) =1 ONLY in blue points, and the value of the function has to be f(m,n)=0 ONLY in red points.
The look of the function isn't important as long as it complies with previous terms.
Homework Equations
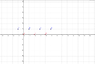
You can see a graphicon with charasteristic points:
In the first example m=2 (m is period).
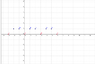
In the next example m=3:
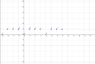
For m=4:
and so on.
The Attempt at a Solution
In first example (for m=2) I used functions: sin and absolute, but for all other m,
it is not possible with only those functions, I also tried use the Fourier series but I don't have so
much knowledge in mathematics to built a such function.
Does somebody know how to do it?
Attachments
Last edited: