General Relativity, Gravity, Help

[Jeebus]

I'm a little confused with the whole idea of matter warping the 'fabric of space.' I'm a sophmore in high school and I'm just in Algebra 2 and pre-calc, so a strict mathematical definition isn't exactly what I'm looking for. In fact, the only knowledge I have about this is based on illustration and brief description. There are two main things I'm confused about.

The Paper Model

It seems like a lot of the illustrations I see for distorted space are shown as warped pieces of paper, or malleable surfaces. I was watching that thing on string theory via the NOVA website the other night and it used the image of the sun as a heavy ball on a trampoline. This confused me because it illustrates space as sitting on one invisible surface. Are illustrations such as these used to show only one of the infinite amount of planes affected by the matter depicted? If so, that makes sense. But that brings me to my next question...

'In' or 'Out'?

Here I have two seemingly contradictory images of how matter affects the space around it. The first is a very common illustration and one I already mentioned, the ball on a trampoline illustration.

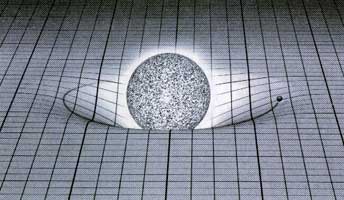
To me, this is showing matter stretching space out around it (the lines curving under the ball to slide around it).

I have a different picture in a book, though. I'm sorry that I can't find anything online resembling it, but it's an image in book called Big Bang: The Story of the Universe by Heather Couper and Niegel Henbest (page 39). It's an illustrated, layman's guide to the Big Bang. Anyway, for those who don't have (access to) it, it shows an illustration of a cube with a massive object in the middle. The object seems to distort the cube by sucking in the space around it (obviously, the space closest to the object is more distorted and the cube shape is gradually reformed as you move away from the object), whereas in the other drawing, the object seemed to distort space in the opposite direction.

The cube model makes more sense to me, but considering the fact that both models seem to be valid/used a lot, I'm assuming that they really are compatible and that the problem is just my understanding of them.

NOTE: If you'd prefer to just explain the subject in general without directly addressing my specific questions, that's fine (but I'd appreciate it if the questions were answered somewhere in the explanation). Suggested reading for someone at my level would be nice, too.

Thanks!

 

[futz]

The image of a ball warping some flat surface is a common way of showing how objects distort space. Of course, the real thing is necessarily 3D, and the distortion occurs all around the object.

 

[LURCH]

Not sure if this will help but;

You can get a more accurate picture from the famous "rubber sheet" analogy by picturing what it would look like if you are looking straight down from above it. This has two major advantages, the first being that the object which appears spherical in the original diagram would look like a disk when viewed from directly above. This makes the illustration more integrated since it is a two-dimensional object on a two-dimensional surface. The other advantage is that, from this angle, the grid lines on the flat surface all appear to curve toward the object from all directions. This is the proper meaning of the rubber sheet analogy, it is a two-dimensional representation of what happens in three dimensions.

On the two-dimensional surface, the disk (as it appears from this angle) represents the heavy ball in the original diagram, perhaps a cannon ball. A smaller ball (like a marble) that tries to roll passed this large ball can only go by in one of the directions afforded by the two dimensions of its environment. That is, it can only go in front or behind or to the left or the right of the cannon ball. But whichever way it's going, its trajectory will be curved toward the cannon ball. Now, even though you can only see the lines running along the two directions (left to right or front and back), in your mind you are aware that the curvature of these lines is a result of the surface being bent in a third direction, up and down.

This, then, is what gravity does to three-dimensional space. It causes a curve in a fourth direction which is at a 90^o angle to the three with which we are commonly familiar.

 

[ranyart]

Read these posts, there is link I provided which may prove interesting:https://www.physicsforums.com/showthread.php?threadid=8274

 

[Adrian Baker]

An illustration of the way 'warping' occurs is to consider setting out on a journey into into space. If you set out in a straight line you wouldn't expect to end up where you started from would you?

However, mass can warp space time, as illustrated by the rubber sheet analogy, and if warped enough you can end up back where you started. It is like a minute creature walking on the surface of a large sphere - it looks flat on his scale, but having walked onwards in a straight line, it would end up back where it started.

(Cosmologists - don't shoot me down here with long complicated discussions about open or closed spacetime - I'm trying to simplify!)

Light follows a straight line path in space, but if mass distorts that spacetime, then it follows a curved path - ie it appears to be attracted by mass.

The warping effect idea can also solve the 'action at a distance' problem of how masses can interact over large distances. There is no Force, just curved paths! This is covered on another thread about Gravitons somewhere...